Formulation and Solution
The motion of electrons, i.e., how the probability distribution of detection coordinate of electron changes over time, is described by the Schrödinger equation:
\[ i \hbar\frac{\partial \psi(x,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \frac{\partial^2 \psi(x,t)}{\partial x^2}+V(x)\psi(x,t). \]
In particular, when the potential is \(\small V(x)=0 \), that is, when the electron is not influenced by other physical objects, it is called a free state. This is how an electron moves when it does not interact with other quanta, and we will try to find how the probability distribution of the coordinates at which an electron is detected changes in this case by solving the Schrödinger equation.
It is generally said that a quantum has uncertainty regarding its coordinates, and if we consider the probability distribution of natural states, it would be a reasonable assumption to assume that it has uncertainty that follows a normal distribution. Therefore, let assume that the probability distribution of quantum coordinates at the initial point in time follows a normal distribution. Such a model is called a Gaussian wave packet model. According to a textbook on quantum mechanics (e.g. Tomonaga [2]), it is assumed that the wave function corresponding to the coordinates and the momentum of the initial state is given as:
\[ \psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right). \]
Here, \(\small \bar{p}\) is the expected value of momentum, and \(\small \sigma \) is the parameter that represents the uncertainty of the observed coordinates. The probability distribution of the observed coordinates follows a normal distribution and it can be written as:
\[ P(x,0)=|\psi(x,0)|^2 = \frac{1}{\sqrt{\pi\sigma^2}} \exp\left(-\frac{x^2}{\sigma^2}\right). \]
From the above, the problem becomes one of finding \(\small \psi(x,t)\) for the motion of an electron in a free state when the fundamental equation and boundary condition are:
\[ \begin{align*} &i \hbar\frac{\partial \psi(x,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \frac{\partial^2 \psi(x,t)}{\partial x^2} \\ &\psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right). \end{align*} \]
If someone said to you, “Here’s a partial differential equation practice problem, solve it quickly,” would you be able to solve it? To show the solution first,
\[ \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x -\frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( x -\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right) \ \end{align*} \]
is the solution (quoted from Tomonaga [2]). By diligently calculating the partial differentials and applying them to the equation, you will be able to confirm that the conditions are met. Therefore,
\[ \begin{align*} P(x,t) \; & = \psi^{\ast}(x)\psi(x) \\ &= \frac{1}{\sqrt{\pi} \sigma \left( 1+\left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)^{1/2}} \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{\sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \end{align*} \]
holds. This is also a normal distribution and let define \(\small N(\mu, \sigma^2) \) as the normal distribution function,
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \;\frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right) \]
is the probability distribution of the observed coordinates of the electron at the time point \(\small t \). “Hey, how did they derive this?” is the subject of this article.
Derivation
The solution in the previous section appears to be derived using a Fourier transform. The boundary condition is Fourier transformed and set as:
\[ \psi(x,0) = \int_{-\infty}^\infty A_k\exp(ikx) dk. \]
This means that the solution can be expressed as a superposition of an infinite number of complex functions, \(\small \psi_k(x,0)=\exp(ikx)\). Let assume
\[ \frac{\partial \psi_k(x,t)}{\partial x} = ik\psi_k(x,t) \]
and substituting into the Schrodinger equation,
\[ \frac{\partial^2 \psi_k(x,t)}{\partial x^2} = -k^2\psi_k(x,t) \]
holds and we get
\[ \frac{\partial \psi_k(x,t)}{\partial t} = -i\frac{\hbar k^2}{2m}\psi_k(x,t). \]
Since
\[ \frac{\partial \ln \psi_k(x,t)}{\partial t} = \frac{1}{\psi_k(x,t)}\frac{\partial \psi_k(x,t)}{\partial t}, \]
by integrating with respect to time, we get
\[ \ln \psi_k(x,t) = -i\frac{\hbar k^2}{2m}t+C. \]
By defining the integral constant \(\small C\) so that the boundary condition is satisfied when \(\small t=0\),
\[ \psi_k(x,t) = \exp\left(ikx-i\frac{\hbar k^2}{2m}t \right) \]
can be obtained. Therefore, \(\small \psi(x,t)\) can be calculated as:
\[ \begin{align*} \psi(x,t) &= \int_{-\infty}^\infty A_k\psi_k(x,t) dk \\ &= \int_{-\infty}^\infty A_k\exp\left(ikx-i\frac{\hbar k^2}{2m}t \right) dk. \end{align*} \]
Using Fourier’s theorem (inverse Fourier transform) from the boundary conditions, we can find the probability amplitude \(\small A_k\) to be:
\[ A_k = \frac{1}{2\pi}\int_{-\infty}^\infty \psi(x,0)\exp(-ikx)dx, \]
and
\[ A_k = \frac{1}{2\pi} \frac{1}{\sigma^{1/2}\pi^{1/4}}\int_{-\infty}^\infty \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right)\exp(-ikx)dx \]
can be obtained. If we complete the square of the integral for \(\small x\), we get
\[ \begin{align*} &\exp\left(-\frac{x^2}{2\sigma^2}+i\left(\frac{\bar{p}}{\hbar}-k\right)x \right) \\ &=\exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) \exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right). \end{align*} \]
Hence,
\[ \begin{align*} &A_k = \frac{1}{2\pi} \frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \\ &\qquad\quad\int_{-\infty}^\infty \exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) dx \end{align*} \]
and the integral can be calculated as:
\[ \begin{align*} &\small \int_{-\infty}^\infty \exp\left(-\frac{\left(x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right)\right)^2}{2\sigma^2} \right) dx = \int_{-\infty}^\infty \exp\left(-\frac{z^2}{2\sigma^2} \right) dz = \sqrt{2\pi\sigma^2} \\ &z = x-i\sigma^2\left(\frac{\bar{p}}{\hbar}-k\right). \end{align*} \]
Although \(\small z\) is a complex number, the last equation seems to hold just as for real numbers (you can understand this by recalling the formula for normal distribution). Therefore,
\[ A_k = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right) \]
can be obtained.
All that remains is to substitute \(\small A_k\) into the equation for \(\small \psi(x,t)\) and calculate the integral. Since
\[ \psi(x,t) = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\int_{-\infty}^\infty \exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ikx-i\frac{\hbar k^2}{2m}t \right) dk, \]
complete the squares and calculate the integral for \(\small k\). It is very complicated, but it can be calculated as:
\[ \begin{align*} &\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ikx-i\frac{\hbar k^2}{2m}t \right) \\ &=\exp \left(-\frac{1}{2}\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(k-\frac{\sigma^2\bar{p}/\hbar+ix}{\sigma^2+\frac{i\hbar t}{m}} \right)^2 \right) \\ &\quad\times \exp \left(-\frac{1}{2\left(\sigma^2+\frac{i\hbar t}{m} \right)}\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right) \right). \end{align*} \]
Since the integral only applies to the completed square, if we recall the calculation of the normal distribution, we can see that
\[ \begin{align*} &\int_{-\infty}^\infty \exp \left(-\frac{1}{2}\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(k-\frac{\sigma^2\bar{p}/\hbar+ix}{\sigma^2+\frac{i\hbar t}{m}} \right)^2 \right) dk \\ &= \sqrt{2\pi}\frac{1}{\sigma\sqrt{1+\frac{i\hbar t}{m\sigma^2}}} \end{align*} \]
holds true. Therefore,
\[ \begin{align*} \psi(x,t) & = \frac{1}{\sigma^{1/2}\pi^{1/4}}\frac{1}{\sqrt{1+\frac{i\hbar t}{m\sigma^2}}} \\ & \times \exp \left(-\frac{1}{2\left(\sigma^2+\frac{i\hbar t}{m} \right)}\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right) \right) \end{align*} \]
can be obtained. Since the contents of \(\exp \) are difficult to understand, we will simplify the equation by multiplying the numerator and denominator by \(\small (\sigma^2-i\hbar t/m) \). The denominator can be calculated as:
\[ 2\left(\sigma^2+\frac{i\hbar t}{m} \right)\left(\sigma^2-\frac{i\hbar t}{m} \right)=2\sigma^4\left(1+\left(\frac{\hbar t}{m\sigma^2}\right)^2\right). \]
The numerator is calculated by separating the real and imaginary terms. Let define the numerator as:
\[ \varphi =-\left(x^2-2i\sigma^2\bar{p}/\hbar\left(x-\frac{\bar{p}}{2m}t\right) \right)\left(\sigma^2-\frac{i\hbar t}{m}\right), \]
then the real part is:
\[ \Re[\varphi]=-\sigma^2\left(x^2-2\frac{\bar{p}}{m}t\left(x-\frac{\bar{p}}{2m}t \right) \right)=-\sigma^2\left(x-\frac{\bar{p}}{m}t \right)^2 \]
and the imaginary part is:
\[ \Im[\varphi] = i\left(\frac{\hbar t}{m} x^2+2\sigma^4\frac{\bar{p}}{\hbar}\left(x-\frac{\bar{p}}{2m}t \right) \right). \]
If this equation is rearranged, it can be calculated as:
\[ \Im[\varphi] =i\left(\frac{\hbar t}{m}\left( x-\frac{\bar{p}}{m}t\right)^2+ 2\sigma^4\left(1+\left(\frac{\hbar t}{m\sigma^2}\right)^2\right)\frac{\bar{p}}{\hbar}\left(x-\frac{\bar{p}}{2m}t \right) \right). \]
Therefore, the final solution can be obtained as:
\[ \begin{align*} \psi(x,t) \; & = \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left( x -\frac{\bar{p}}{m}t \right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x -\frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left( x -\frac{\bar{p}}{m}t \right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right), \end{align*} \]
as shown in the previous section.
In the Case of Photons
We calculated the probability distribution for the coordinates of a free electron, but let us use a similar method to calculate the probability distribution for the coordinates of a photon. In the case of photons, readers with a knowledge of electromagnetism might assume that the fundamental equations are the Maxwell-Hertz equations (the fundamental equations of electromagnetic waves):
\[ \frac{1}{c^2}\frac{\partial^2 \psi(x,y,z,t)}{\partial t^2}=\frac{\partial^2 \psi(x,y,z,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,z,t)}{\partial y^2}+\frac{\partial^2 \psi(x,y,z,t)}{\partial z^2}. \]
However, in fact, it is known that in relativistic quantum mechanics, this fundamental equation does not work well as an equation describing the time evolution of the photon wave function. Strictly speaking, the fundamental equation is:
\[ \frac{1}{c}\frac{\partial \psi(x,y,z,t)}{\partial t}=\gamma_1\frac{\partial \psi(x,y,z,t)}{\partial x}+\gamma_2\frac{\partial \psi(x,y,z,t)}{\partial y}+\gamma_3\frac{\partial \psi(x,y,z,t)}{\partial z}, \]
which is replaced by a first-order partial differential equation using coefficients that satisfy
\[ \gamma_i^2=1, \gamma_i\gamma_j=0, \quad i,j = 1,2,3, \]
which is called the Dirac matrices. By squaring both sides, we can eliminate the Dirac matrices and express it as:
\[ \small \frac{1}{c^2}\left(\frac{\partial \psi(x,y,z,t)}{\partial t}\right)^2=\left(\frac{\partial \psi(x,y,z,t)}{\partial x}\right)^2+\left(\frac{\partial \psi(x,y,z,t)}{\partial y}\right)^2+\left(\frac{\partial \psi(x,y,z,t)}{\partial z}\right)^2. \]
Of course, calculations are difficult in the three-dimensional case, so let us find the probability distribution for the coordinates of a photon when space is one-dimensional. Just like the Schrödinger equation, we need to find \(\small \psi(x,t)\) when the fundamental equation and boundary condition are:
\[ \begin{align*} &\frac{1}{c^2}\frac{\partial \psi(x,t)}{\partial t}\frac{\partial \psi^{\ast}(x,t)}{\partial t}=\frac{\partial \psi(x,t)}{\partial x}\frac{\partial \psi^{\ast}(x,t)}{\partial x} \\ &\psi(x,0) = \frac{1}{\sigma^{1/2}\pi^{1/4}} \exp\left(-\frac{x^2}{2\sigma^2}\right) \exp \left( \frac{i}{\hbar} \bar{p} x \right). \end{align*} \]
Note that since \(\small \psi(x,t)\) is a complex function, the square is calculated by multiplying with the complex conjugate. If the energy of a photon is:
\[ E^2 = p^2c^2 \; \Rightarrow \; EE^\ast=(pc)(pc)^\ast, \]
then this is a basic equation that can be derived from the correspondence principle.
The boundary condition is Fourier transformed and set as:
\[ \psi(x,0) = \int_{-\infty}^\infty A_k\exp(ikx) dk. \]
Let assume
\[ \frac{\partial \psi_k(x,t)}{\partial x} = ik\psi_k(x,t) \]
and substitute into the fundamental equation,
\[ \frac{\partial \psi_k(x,t)}{\partial t} = \pm ick\psi_k(x,t) \]
can be obtained. Since there are two signs, let us assume that the signs are determined randomly with probability \(\small 1/2\). In this case, by integrating with respect to time, setting the integral constant \(\small C \) so that the boundary condition is satisfied when \(\small t=0 \), and putting it as:
\[ \psi_k(x,t) = \frac{1-i}{2}\exp\left(ik(x-ct) \right)+\frac{1+i}{2}\exp\left(ik(x+ct) \right), \]
we can confirm \(\small \psi_k(x,0)=\exp(ikx)\). The coefficients are determined so that when multiplied by the complex conjugate, the cross terms cancel out and each term becomes \(\small 1/2\). The Fourier transform of the boundary condition is:
\[ A_k = \frac{\sigma}{\sqrt{2\pi}}\frac{1}{\sigma^{1/2}\pi^{1/4}}\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2\right), \]
as in the previous section.
Now we just need to calculate
\[ \psi(x,t) = \int_{-\infty}^\infty A_k\psi_k(x,t) dk. \]
By completing the square for \(\small k \), we get
\[ \begin{align*} &\exp\left(-\frac{\sigma^2}{2}\left(\frac{\bar{p}}{\hbar}-k\right)^2+ik(x\pm ct) \right) \\ &=\exp \left(-\frac{\sigma^2}{2}\left(k-\frac{\sigma^2\bar{p}/\hbar+i(x\pm ct)}{\sigma^2} \right)^2 \right) \\ &\quad\times \exp \left(-\frac{1}{2\sigma^2}\left(\left(x\pm ct \right)^2-2i\sigma^2\bar{p}/\hbar\left(x\pm ct\right) \right) \right) \end{align*} \]
Since the integral only applies to the completed square, if we recall the calculation of the normal distribution, we can see that
\[ \int_{-\infty}^\infty \exp \left(-\frac{\sigma^2}{2}\left(k-\frac{\sigma^2\bar{p}/\hbar+i(x\pm ct)}{\sigma^2} \right)^2 \right) dk = \frac{\sqrt{2\pi}}{\sigma} \]
holds true. Therefore,
\[ \begin{align*} \psi(x,t)= \frac{1}{\sigma^{1/2}\pi^{1/4}} & \Biggl[ \frac{1-i}{2} \exp \left(-\frac{\left(x- ct \right)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}(x-ct) \right) \\ &+\frac{1+i}{2}\exp \left(-\frac{\left(x+ct \right)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}(x+ct) \right) \Biggr] \end{align*} \]
can be obtained. Calculating the probability distribution we get
\[ P(x,t) = |\psi(x,t)|^2 = \frac{1}{2}\frac{1}{\sqrt{\pi\sigma^2}}\left[\exp \left(-\frac{\left(x- ct \right)^2}{\sigma^2} \right)+\exp \left(-\frac{\left(x+ ct \right)^2}{\sigma^2} \right) \right]. \]
This probability distribution seems intuitively reasonable when we consider that the speed of a photon must be constant, the speed of light \(\small c\). However, it is known that photons have discrete observable physical quantities, such as energy, and it should be noted that there may be some constraints (discreteness) on the observable \(\small (x,t) \) strictly speaking. Also, the time \(\small t \) here is different from the time we perceive, so the calculation result may not be meaningful.
Quantum Motion Is Not Brownian Motion
The content of this article ends with the previous section, but I would like to conclude with a short story that will also serve as an advertisement for the book I wrote. In fact, the desire to describe quantum motion as a stochastic process has existed for a long time. It seems that Schrödinger himself rejected the theory of the probabilistic interpretation of the wave function proposed by Max Born, and he came up with the thought experiment of Schrödinger’s cat to refute this theory. Schrödinger seems to have believed that if the probabilistic interpretation of the wave function is correct, then it would be strange if quantum motion could not be described by a stochastic equation of motion (i.e., a stochastic process).
The idea of describing quantum motion using this stochastic equation of motion was inherited by Richard P. Feynman, and the theory he constructed known as the path integral. However, path integrals have been strongly criticized by mathematicians, and are said to be a theory lacking a mathematical foundation, in the sense that it involves arbitrarily calculating integrals that cannot be mathematically defined (calculated) so that the results match. It seems that the problem of providing a mathematical foundation for this path integral remains unsolved to this day (although the author is not sure whether this is true or not).
However, due to the rapid development of the theory of stochastic integrals and stochastic differential equations related to Brownian motion, which was developed by the Japanese mathematician Kiyoshi Ito in the 1940s, it seems that some thought was given to whether the theory of Brownian motion could provide a mathematical foundation for path integrals. Feynman himself appears to have been working with mathematician Mark Kac to research whether the theory of Brownian motion could be used to construct a theory of path integrals (the Feynman-Kac formula is said to have been devised during this research). Even today, research continues to attempt to describe the theory of quantum mechanics using Brownian motion and stochastic differential equations, and countless papers can be found on the Internet and in academic journals.
However, as shown in this article, the solution to the Schrödinger equation represents a probability distribution:
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \;\frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right), \]
which is clearly different from the probability distribution of Brownian motion. If it is Brownian motion, it would have to be:
\[ x(t) \sim N\left(\frac{\bar{p}}{m}t, \; \frac{\hbar}{m}t \right). \]
Another way of thinking about this is to set \(\small \bar{p}=0\) in the solution to the Schrödinger equation and take only the imaginary part, which can be expressed as:
\[ K(x,t) = \exp \left(i \left\{ \frac{\hbar t x ^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right). \]
For the denominator, we can approximate it by assuming that it is \(\small (\hbar t /m\sigma^2)^2 \gg 1\) and adjust the constant part to express it as:
\[ K(x,t) = \frac{1}{\sqrt{2\pi\frac{i\hbar}{m}t}} \exp \left(- \frac{x ^2}{2 \frac{i\hbar}{m}t} \right). \]
This equation can be expressed as the heat conduction equation:
\[ \frac{\partial K(x,t)}{\partial t} = \frac{i\hbar}{2m} \frac{\partial^2 K(x,t)}{\partial x^2}. \]
If we multiply both sides by \(\small i\hbar\), we get
\[ i\hbar\frac{\partial K(x,t)}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^2 K(x,t)}{\partial x^2}, \]
which looks a bit like the Schrödinger equation. This has led to the idea that quantum motion may be described using Brownian motion, where time, mass, or volatility is imaginary. However, this is just an analogy, and the wave function is not itself a probability distribution function, so there is no point in making such calculations.
From the above considerations, it can be seen that the idea of using Brownian motion to construct a theory of quantum mechanics and to provide a mathematical foundation for path integrals is flawed at a fundamental level. If you have the ambition to learn the theory of Brownian motion and quantum mechanics and link the two to construct the theory of quantum mechanics, I would like to point out that it is a waste of time and you should give up. Well, I don’t know about those who have been studying for years or even decades and can’t be undone…
So, does this mean that it is impossible to construct the theory of quantum mechanics using stochastic processes? The author believes this is not the case either. However, in order to construct this theory, we must deny certain assumptions that we have come to believe are true so unconditionally, which is not easy to notice, and even if we did, it is difficult to accept. In other words, this assertion makes it clear that if you think you understand quantum mechanics, you really don’t understand it. If you are interested in these theories, I recommend you take a look at the author’s book [3, 4]. Finally, I will ignore the criticism that I just wanted to write a long article to promote my book…
Reference
[1] Tomonaga, Shin-ichiro (1962). Quantum Mechanics Volume 1:Old Quantum Theory. North-Holland.
[2] Tomonaga, Shin-ichiro (1966). Quantum Mechanics Volume 2:New Quantum Theory. John Wiley & Sons (Interscience Publishing).
[3] Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.
[4] Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.
[5] Feynman, Richard. P. and Albert. R. Hibbs (1965), Quantum Mechanics and Path Integrals, McGraw-Hill, Inc.
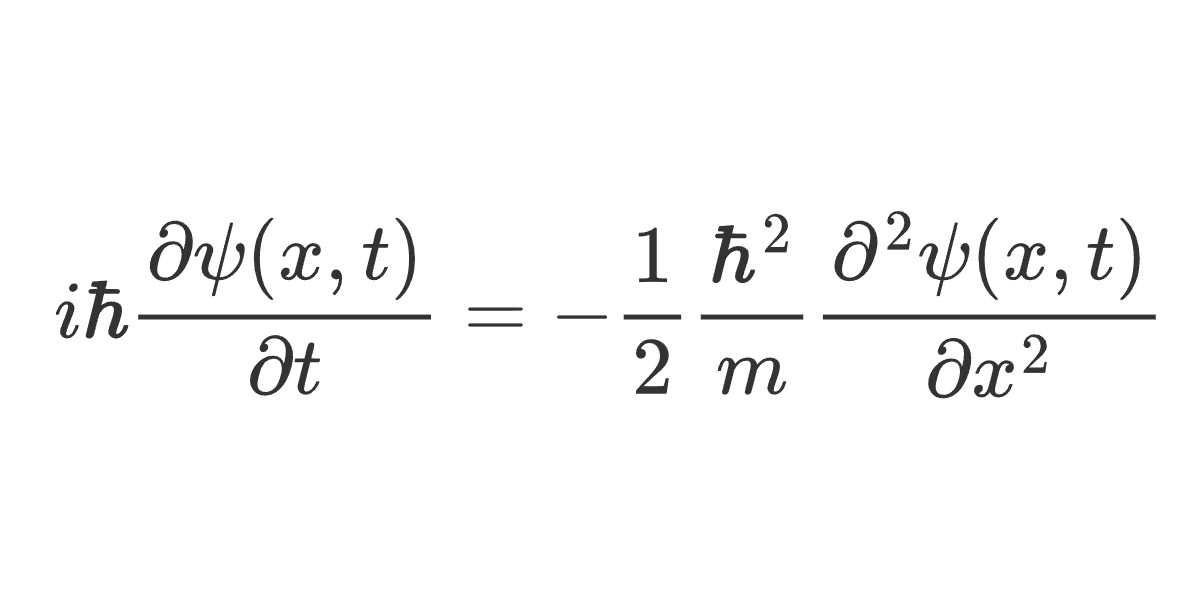


Comments