Energy and Potential in the Theory of Relativity
We have considered elliptical motion in classical mechanics in several articles, but let us consider extending this to the framework of the theory of relativity. The energy of elliptical motion in classical mechanics is:
\[ \small E = \frac{p^2}{2m}-\frac{GmM}{r} = -\frac{1}{2}\frac{GmM}{a}, \]
and let us put this into the form of the relativistic energy equation:
\[ \small E^2 = m^2c^4+p^2c^2+EV. \]
If we add \(\small mc^2\) to the energy equation in classical mechanics and convert it into a square root equation, we get
\[ \small \begin{align*} E &= mc^2+\frac{p^2}{2m}-\frac{GmM}{r} \\ &\approx \sqrt{m^2c^4+p^2c^2-mc^2\frac{2GmM}{r}}. \end{align*} \]
By replacing \(\small mc^2\) which is multiplied to the potential with \(\small E\), the potential function in the theory of relativity can be obtained as:
\[ \small V = -\frac{2GmM}{r}. \]
Therefore, energy in the theory of relativity can be expressed as:
\[ \small E^2 = m^2c^4+p^2c^2-E\frac{2GmM}{r}. \]
Furthermore, according to the equivalence principle in general relativity, the mass on which gravity acts is relativistic mass \(\small m=E/c^2\), so the gravitational mass \(\small m\) in the potential function must be distinguished from the rest mass \(\small m\). Hence, the energy equation must be expressed as:
\[ \small E^2 = m^2c^4+p^2c^2-\frac{E^2}{c^2}\frac{2GM}{r}. \]
By solving the equation for \(\small E\), we get
\[ \small E = \sqrt{\frac{m^2c^4+p^2c^2}{1+\frac{2GM}{c^2r}}}. \]
It is easy to understand that energy in classical mechanics can be approximated as:
\[ \small \begin{align*} E &= \sqrt{\frac{m^2c^4+p^2c^2}{1+\frac{2GM}{c^2r}}}-mc^2 \approx\sqrt{m^2c^4+p^2c^2}\left(1-\frac{GM}{c^2r} \right) -mc^2 \\ &\approx mc^2+\frac{p^2}{2m}-\frac{GmM}{r}. \end{align*} \]
The puzzling thing about reconciling this with classical mechanics is that the potential value is doubled. Of course, the radius of an orbit in relativity would not be half the radius of an orbit in classical mechanics. This is due to the difference between the method of deriving the equations of motion in classical mechanics and that in the theory of relativity. In classical mechanics, the calculation was done as
\[ \small \frac{d^2x}{dt^2} = -\frac{GM}{r^3}x, \]
but in the theory of relativity, it is necessary to calculate it using the time derivative of momentum. In other words, it is necessary to derive the equation of motion from the assumption that
\[ \small \frac{dp_x}{dt} = -\frac{GM}{r^3}x. \]
This means that the operation of differentiating the potential function with respect to coordinates to obtain the equation of motion cannot be applied to the theory of relativity.
So what effect does doubling the potential have? Let us calculate how the potential function:
\[ \small V =x\frac{dp_x}{dt}+y\frac{dp_y}{dt}+z\frac{dp_z}{dt}+c^2T\frac{dm}{dt} \]
in the conical coordinate system relates to the above calculation. The sum of the first three terms can be found to be
\[ \small x\frac{dp_x}{dt}+y\frac{dp_y}{dt}+z\frac{dp_z}{dt} = -\frac{E}{c^2}\frac{GM}{r}. \]
Since
\[ \small V = -\frac{E}{c^2}\frac{2GM}{r}, \]
if
\[ \small c^2T\frac{dm}{dt} = \frac{E}{c^2}c^2T\frac{d^2T}{dt^2} = -\frac{E}{c^2}\frac{GM}{r} \]
is true, then the above formula is true. This is the equation of motion that local time \(\small T_{xyzt}\) must satisfy. Since this equation does not hold for \(\small dm/dt=0\), it may follow that the assumption that rest mass \(\small m\) is a constant cannot be justified by the theory of relativity. From the above, we can conclude that the potential function of the theory of relativity is twice as large as that of classical mechanics because an extra term, \(\small c^2T(dm/dt)\), is added, and that this term contributes to the potential function in the same direction as the \(\small xyz\) coordinate axes.
Equation of Motion for Elliptical Motion
Let us find the equation of motion corresponding to the energy calculated above. Since we defined momentum as:
\[ \small p_\mu = \frac{E}{c^2}\frac{dq_\mu}{dt}, \]
we get
\[ \small \frac{dq_\mu}{dt} = \frac{p_\mu c^2}{E} = \frac{p_\mu c^2}{\sqrt{ m^2c^4+p^2c^2}}\sqrt{1+\frac{2GM}{c^2r}}. \]
Differentiating again with respect to time gives
\[ \small \begin{align*} \frac{d^2q_\mu}{dt^2} = & \frac{c^2}{\sqrt{ m^2c^4+p^2c^2}}\sqrt{1+\frac{2GM}{c^2r}}\frac{dp_\mu}{dt} \\ & -\frac{p_x c^2}{\sqrt{ m^2c^4+p^2c^2}^3}\sqrt{1+\frac{2GM}{c^2r}}\left[\left(p_x\frac{dp_x}{dt}+p_y\frac{dp_y}{dt}+p_z\frac{dp_z}{dt}+mc^2\frac{dm}{dt}\right)c^2 \right] \\ & -\frac{p_\mu c^2}{\sqrt{ m^2c^4+p^2c^2}}\frac{GM}{c^2r^2\sqrt{1+\frac{2GM}{c^2r}}}\frac{dr}{dt}. \end{align*} \]
If we substitute the formula for the time derivative of momentum and calculate it well, we get
\[ \small \begin{align*} \frac{d^2q_\mu}{dt^2} = &-\frac{GM}{r^3}q_\mu+\frac{GM}{r^3}\frac{p_\mu}{E^2}\frac{1}{1+\frac{2GM}{c^2r}}\left[\left(p_xx+p_yy+p_zz+m\frac{r^2}{T}\right)c^2 \right] \\ &-\frac{p_\mu c^2}{E}\frac{GM}{c^2r^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dr}{dt}. \end{align*} \]
When momentum is converted to velocity, it becomes
\[ \small \begin{align*} \frac{d^2q_\mu}{dt^2} = &-\frac{GM}{r^3}q_\mu+\frac{GM}{c^2r^3}\frac{dq_\mu}{dt}\frac{1}{1+\frac{2GM}{c^2r}}\left[x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt}+\frac{r^2}{T}\frac{dT}{dt} \right] \\ & -\frac{GM}{c^2r^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dq_\mu}{dt}\frac{dr}{dt}. \end{align*} \]
Since
\[ \small x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} = r\frac{dr}{dt}, \]
The second term related to coordinates and the third term can be canceled out to get
\[ \small \frac{d^2q_\mu}{dt^2} = -\frac{GM}{r^3}q_\mu+\frac{GM}{c^2r^3}\frac{dq_\mu}{dt}\frac{1}{1+\frac{2GM}{c^2r}}\frac{r^2}{T}\frac{dT}{dt}. \]
This is the equation of motion for elliptical motion in the theory of relativity. This can also be applied to the coordinate axis \(\small T\).
From the above, it follows that elliptical motion in the theory of relativity obeys simultaneous differential equation:
\[ \small \begin{align*} &\frac{d^2x}{dt^2} = -\frac{GM}{r^3}\left(x-\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dx}{dt}\frac{r^2}{T}\frac{dT}{dt}\right) \\ &\frac{d^2y}{dt^2} = -\frac{GM}{r^3}\left(y-\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dy}{dt}\frac{r^2}{T}\frac{dT}{dt}\right) \\ &\frac{d^2z}{dt^2} = -\frac{GM}{r^3}\left(z-\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dz}{dt}\frac{r^2}{T}\frac{dT}{dt}\right) \\ &\frac{d^2T}{dt^2} = -\frac{GM}{r^3}\left(\frac{r^2}{c^2T}-\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{r^2}{T}\left(\frac{dT}{dt}\right)^2\right). \end{align*} \]
It is likely that this system of differential equations cannot be solved analytically, so a solution will need to be found through numerical calculations. I will briefly explain the numerical solution of simultaneous differential equations later.
Also, the above solution requires the absolute value of \(\small T,t\), which is an unobservable value and the true numerical value cannot be known. Therefore, let us apply the approximation \(\small t=0\), as in the general theory of relativity. Since it was
\[ \small \begin{align*} &r^2+c^2T^2 = c^2t^2 \\ &r\frac{dr}{dt}+c^2T\frac{dT}{dt} = c^2t \end{align*} \]
in the conic coordinate system, if \(\small t=0\), then
\[ \small \begin{align*} &r^2 = -c^2T^2 \\ &r\frac{dr}{dt} = -c^2T\frac{dT}{dt} \end{align*} \]
holds true. By substituting the above equation into the below equation, we can get
\[ \small \frac{dT}{dt} = \pm \frac{T}{r}\frac{dr}{dt}. \]
Although it may be arbitrary, if we take the negative solution and substitute this equation into the equation of motion and rearrange, we get
\[ \small \begin{align*} &\frac{d^2x}{dt^2} = -\frac{GM}{r^3}\left(x+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dx}{dt}r\frac{dr}{dt}\right) \\ &\frac{d^2y}{dt^2} = -\frac{GM}{r^3}\left(y+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dy}{dt}r\frac{dr}{dt}\right) \\ &\frac{d^2z}{dt^2} = -\frac{GM}{r^3}\left(z+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dz}{dt}r\frac{dr}{dt}\right) \\ &\frac{d^2T}{dt^2} = -\frac{GM}{r^3}\left(\frac{r^2}{c^2T}+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}T\left(\frac{dr}{dt}\right)^2\right). \end{align*} \]
Since we have eliminated \(\small T\) from the equation of motion for \(\small x,y,z\), we can omit the equation relating to \(\small T\). By converting the equation for \(\small r(dr/dt)\) into the equation for \(\small x,y,z\), we can calculate
\[ \small \begin{align*} &\frac{d^2x}{dt^2} = -\frac{GM}{r^3}\left(x+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dx}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right) \\ &\frac{d^2y}{dt^2} = -\frac{GM}{r^3}\left(y+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dy}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right) \\ &\frac{d^2z}{dt^2} = -\frac{GM}{r^3}\left(z+\frac{1}{c^2}\frac{1}{1+\frac{2GM}{c^2r}}\frac{dz}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right). \end{align*} \]
This is the formula for elliptical motion in the theory of relativity. The difference from classical mechanics would be that it would be a term similar to the magnetic field in electromagnetism. Since this equation is based on the premise that \(\small t=0\), it is important to note that when actually performing the calculation, even if time is advanced by differential calculation, in the next step it is necessary to start over with \(\small t=0\). This is the same as in the usual general theory of relativity.
Finally, let us apply this solution to the equation of motion in the conical coordinate system:
\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2+c^2\left(\frac{dT}{dt}\right)^2+x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2} = c^2. \]
By substituting and rearranging, we get
\[ \small x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2}= -\frac{2GM}{r}-\frac{GM}{c^2r}\frac{1}{1+\frac{2GM}{c^2r}}\left(\left(\frac{dr}{dt}\right)^2+\frac{c^2T^2}{r^2}\left(\frac{dr}{dt}\right)^2\right). \]
In the conical coordinate system at \(\small t=0\), \(\small r^2 = -c^2T^2\), so the second term is zero. Therefore, it seems that consistency would be achieved with format:
\[ \small x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2}= -\frac{2GM}{r}. \]
Schwarzschild Solution
Some readers who have read this far may be frustrated and wondering why a different solution is being derived when the problem setting is the same as the Schwarzschild solution in the general theory of relativity. This is because the discussion up to the previous section has taken the coordinates of the heavier mass point (fixed star) as the origin, in accordance with classical mechanics. In the general theory of relativity, the coordinates of the lighter mass (planet) are taken as the origin, and motion is described in terms of how that mass moves away from the origin. Therefore, the sign of the potential function is opposite, which is:
\[ \small V = \frac{2GmM}{r}. \]
Therefore, in the usual general theory of relativity, it is necessary to derive the equation of motion assuming that the energy is:
\[ \small E = \sqrt{\frac{m^2c^4+p^2c^2}{1-\frac{2GM}{c^2r}}}. \]
If we solve for the equation of motion using the same procedure as in the previous section, we get
\[ \small \begin{align*} &\frac{d^2x}{dt^2} = \frac{GM}{r^3}\left(x+\frac{1}{c^2}\frac{1}{1-\frac{2GM}{c^2r}}\frac{dx}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right) \\ &\frac{d^2y}{dt^2} = \frac{GM}{r^3}\left(y+\frac{1}{c^2}\frac{1}{1-\frac{2GM}{c^2r}}\frac{dy}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right) \\ &\frac{d^2z}{dt^2} = \frac{GM}{r^3}\left(z+\frac{1}{c^2}\frac{1}{1-\frac{2GM}{c^2r}}\frac{dz}{dt}\left(x\frac{dx}{dt}+y\frac{dy}{dt}+z\frac{dz}{dt} \right)\right) \end{align*} \]
(the only difference between the energy equation and the sign is that it is reversed).
In addition, since general relativity does not deal with the concept of potential relative to the \(\small T\) axis, relativistic correction terms in the equations of motion must also be included in the potential function. Hence, the potential function must be calculated as:
\[ \small \frac{c^2}{E}V = 2\left(x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}\right)=\frac{2GM}{r}+\frac{2GM}{c^2r}\frac{1}{1-\frac{2GM}{c^2r}}\left(\frac{dr}{dt}\right)^2. \]
Let us apply this to the equation of motion:
\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2+c^2\left(\frac{dT}{dt}\right)^2+x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2} = c^2 \]
in the conical coordinate system. Multiply both sides by \(\small dt^2\) to express as:
\[ \small dx^2+dy^2+dz^2+c^2dT^2+\left(x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2}\right)dt^2 = c^2dt^2. \]
Replacing
\[ \small \frac{c^2}{E}V = x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2}=\frac{2GM}{r}+\frac{2GM}{c^2r}\frac{1}{1-\frac{2GM}{c^2r}}\left(\frac{dr}{dt}\right)^2 \]
with the term corresponding to acceleration gives us
\[ \small dx^2+dy^2+dz^2+c^2dT^2+\frac{2GM}{r}dt^2+\frac{2GM}{c^2r}\frac{1}{1-\frac{2GM}{c^2r}}dr^2 = c^2dt^2. \]
Also, from polar coordinate calculations, \(\small dx^2+dy^2+dz^2\) can be converted to polar form:
\[ \small \begin{align*} &x = r \sin \theta \cos \varphi \\ &y = r \sin \theta \sin \varphi \\ &z = r \cos \theta \ \end{align*} \]
and expressed as:
\[ \small dx^2+dy^2+dz^2 = dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2. \]
By substituting, we get
\[ \small dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2-c^2dt^2+\frac{2GM}{r}dt^2+\frac{2GM}{c^2r}\frac{1}{1-\frac{2GM}{c^2r}}dr^2 = -c^2dT^2. \]
By rearranging the equation with
\[ \small 1+\frac{2GM}{c^2r}\frac{1}{1-\frac{2GM}{c^2r}} =\frac{1}{1-\frac{2GM}{c^2r}}, \]
it can be summarized as:
\[ \small -c^2dT^2 =-c^2\left(1-\frac{2GM}{c^2r} \right) dt^2+\frac{1}{1-\frac{2GM}{c^2r}}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2. \]
This is a solution known as the Schwarzschild solution. If we think about it this way, we can understand that the equations of motion in the previous section are equivalent to the Schwarzschild solution, although in a different form.
Summery
There are still some parts where my understanding is uncertain (I am not confident about the coefficient (whether to multiply by 2 or not) and the sign (\(\small \pm\))), but it seems to me that I have been able to make the nonlinear equations of motion in the conical coordinate system consistent with the equations of motion in the general theory of relativity. I would like to extend this to problems that simultaneously deal with the motion of multiple substances, such as general gravitational potentials (Newton’s gravitational equation or Einstein’s equation), two-body problems, and three-body problems, but this is likely to be a time consuming story…When dealing with multiple masses, we do not want to restart (reset) time, so we need to calculate \(\small T\) for each mass to satisfy
\[ \small r_i^2+c^2T_i^2 = c^2t^2, \]
but if we start from \(\small t=0\), this means that this has to be a complex number. For example, instead of
\[ \small \begin{align*} &\frac{d}{dt}T^2 = 2T\frac{dT}{dt} \\ &\frac{d^2}{dt^2}T^2 = 2\left(\frac{dT}{dt}\right)^2+2T\frac{d^2T}{dt^2}, \end{align*} \]
it may need to calculate
\[ \small \begin{align*} &\frac{d}{dt}TT^\ast = T^\ast\frac{dT}{dt}+T\frac{dT^\ast}{dt} \\ &\frac{d^2}{dt^2}TT^\ast = 2\frac{dT^\ast}{dt}\frac{dT}{dt}+T^\ast\frac{d^2T}{dt^2}+T\frac{d^2T^\ast}{dt^2}. \end{align*} \]
I think that the theory will eventually take local time as a complex number, but I can’t imagine it at the moment. I have a feeling that it would be enough to set the initial value to \(\small t=\max{r_i/c}\)…
By the way, the space inside the Schwarzschild radius:
\[ \small r_s = \frac{2GM}{c^2} \]
is called a black hole, and the usual general theory of relativity states that once matter enters this radius, it is impossible for it to escape. However, if we use the solution in Section 2, the influence of the relativistic term (which can be seen as the term that pushes matter away due to the centrifugal force caused by rotational motion) becomes greater than the term of gravitational attraction, which means that it is impossible to enter the interior of a black hole in the first place. In this sense, it is important to note that in the theory of relativity, gravity is not a simple attractive force (central force).
Finally, note that in a space with gravity the speed of light is not constant in the Euclidean space sense. In
\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2+c^2\left(\frac{dT}{dt}\right)^2+x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2}+c^2T\frac{d^2T}{dt^2} = c^2, \]
we need only consider the case where \(\small T=0\), which is the condition:
\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2+x\frac{d^2x}{dt^2}+y\frac{d^2y}{dt^2}+z\frac{d^2z}{dt^2} = c^2 \]
that the motion of light must satisfy. However, this may not necessarily mean that the speed of light is not constant. In other words, this equation arises from the condition that it must remain in a conical coordinate system:
\[ \small x^2+y^2+z^2+c^2T^2=c^2t^2, \]
and if we consider that the coordinate of light must be:
\[ \small x^2+y^2+z^2=c^2t^2, \]
then when considering the speed in the conical coordinate system, we must consider that local time \(\small T\) is determined so that the speed of light is constant at \(\small c\). That is, the principle of the constancy of the speed of light in special relativity states that “the speed of light in Euclidean space is constant,” but in general relativity this may be rewritten as “the speed of light in a conical coordinate system is constant.” In a space without gravity, the two simply happen to coincide.


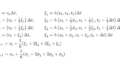
Comments