※The painter ChatGPT “A cyberpunk-inspired futuristic clock set in a high-tech cityscape.”
Introduction
In “Complex Functions and Schrödinger Equation,” the author explained that in a conical coordinate system:
\[ \small x^2+y^2+z^2+c^2T^2 = c^2t^2, \]
if space-time is defined as:
\[ \small \sqrt{x^2+y^2+z^2}+icT = cte^{i\theta}=c\zeta \]
and expressed as:
\[ \small c^2\zeta\zeta^{\ast} =x^2+y^2+z^2+c^2T^2 = c^2t^2, \]
the concept of time in this space-time can be defined as:
\[ \small \zeta = te^{i\theta}. \]
I then argued that if we assume the principle of the constancy of the speed of light, this results in a concept of time that prohibits reversal. However, it seems that the author did not fully understand this way of thinking (and still does not understand it).There may be some readers who find this confusing, so the purpose of this article is to provide additional explanation.
Time Progresses in a Spiral Motion on the Complex Plane (Two-dimensional Space)
Uniform circular motion in a two-dimensional plane \(\small R^2\) can be expressed as:
\[ \small \begin{align*} &x(t) = r\cos (\omega t) \\ &y(t) = r\sin (\omega t). \end{align*} \]
If we represent this on the complex plane, it can be expressed as:
\[ \small x(t)+y(t)i = re^{i\omega t}. \]
This equation expresses uniform circular motion in a complex plane.
Since the concept of time in the conical coordinate system is:
\[ \small \zeta = t\exp\left(-i\frac{E}{\hbar} t\right) = t\exp\left(i\omega t\right), \]
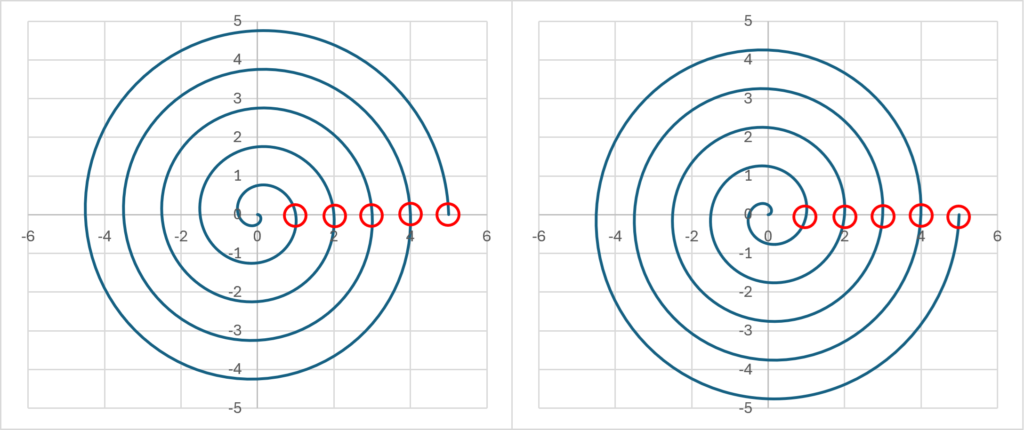
it corresponds to spiral motion in the two-dimensional plane \(\small R^2\). When \(\small E>0,\omega<0\), the motion is clockwise (left graph), and when \(\small E<0,\omega>0\), the motion is counterclockwise (right graph). The specific graph is as follows.

In quantum mechanics, quanta for which time progresses counterclockwise (i.e., \(\small E<0)\) are called antiparticles. Note that time is not going backwards, just that the direction of rotation is reversed. If we assume that the time observed in reality is only real values, then what we can perceive as time is only the points indicated by the red circles below. The time we perceive is discrete, and one could consider the hypothesis that this is the reason why the physical quantities observed in quantum mechanics have discrete values.
Length of Time
If we think as discussed in the previous section, it follows that the physical flow of time may be different from the constant speed that we perceive time to flow \(\small \Delta t, 2\Delta t, \cdots\). This means that the complex time rotates once in the course of \(\small \Delta t\) time, and the actual passage of time may have to be measured as the path length of this spiral motion. In the diagram below, the length of time flowing for each section with a different color is different, so let us calculate what this value is.
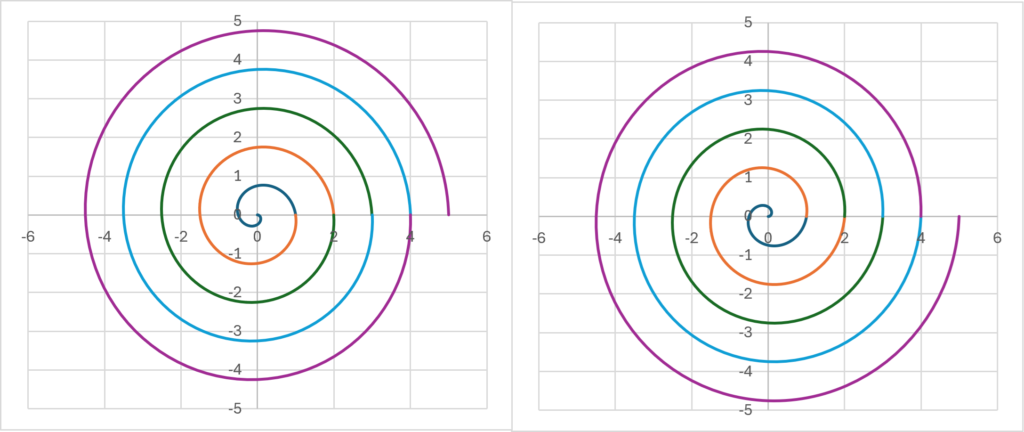
If we consider the complex plane as a two-dimensional Euclidean space, time \(\small \zeta(t)=te^{i\omega t}=x(t)+y(t)i\) can be expressed as:
\[ \small \begin{align*} &x(t) = t \cos \omega t \\ &y(t) = t \sin \omega t. \end{align*} \]
Differentiating with respect to \(\small t\) gives us
\[ \small \begin{align*} &\frac{dx}{dt} = \cos\omega t – \omega t \sin \omega t \\ &\frac{dy}{dt} = \sin\omega t + \omega t \cos \omega t. \end{align*} \]
The path length to time \(\small t\) can be calculated as:
\[ \small \int_0^t \sqrt{\left(\frac{dx}{du}\right)^2+\left(\frac{dy}{du}\right)^2} du. \]
Since
\[ \small \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2 = 1+\omega^2t^2 \]
holds true,
\[ \small T(t) = \int_0^t \sqrt{1 + \omega^2u^2} du \]
is the path length. By calculating this integral, we can get
\[ \small \begin{align*} \int_0^t \sqrt{1+\omega^2u^2}du & = \frac{1}{2\omega}\left(\omega t\sqrt{\omega^2t^2+1}+\sinh^{-1}(\omega t) \right) \\ & = \frac{1}{2\omega}\left(\omega t\sqrt{\omega^2t^2+1}+\log(\omega t+\sqrt{\omega^2t^2+1}) \right). \end{align*} \]
Let us denote the discrete time interval we are aware of as \(\small \Delta t\) and calculate the path length in the interval \(\small [n\Delta t, (n+1)\Delta t]\). We will present the exact values later, but for now let us approximate them as follows. Since the second term is of the logarithmic order, we can ignore it and get
\[ \small \int_{n\Delta t}^{(n+1)\Delta t} \sqrt{1+\omega^2u^2}du \approx \left[\frac{1}{2\omega}\omega^2t^2 \right]^{(n+1)\Delta t}_{n \Delta t} = \left(n + \frac{1}{2}\right)\omega\Delta t \]
by approximating it as \(\small \sqrt{\omega^2t^2+1} \approx \omega t\). In other words, while we perceive the passage of time as \(\small \Delta t, 2\Delta t, \cdots, n\Delta t\), physical time \(\small T(t)\) progresses by just
\[ \small \Delta T(t) = \left(n + \frac{1}{2}\right)\omega\Delta t. \]
This might also be expressed as:
\[ \small \frac{\Delta T(t)}{\Delta t} = \left(n+\frac{1}{2} \right)\omega. \]
The hypothesis that I put forward in “Complex Functions and Schrödinger Equation” was that there may be some connection between this and the energy of the electromagnetic field (light) in quantum mechanics.
By the way, it should be noted that if you perform the above integral calculation strictly, it will not be exactly \(\small 1/2,3/2,5/2.\cdots\) and slight errors will occur. The actual numerical values are as follows (\(\small \Delta T\) has been converted to \(\small 2n+1\) for ease of comparison):
| n | ΔT |
|---|---|
| 0 | 1.07685644147312 |
| 1 | 3.0174979418948 |
| 2 | 5.01025943726294 |
| 3 | 7.00728317754737 |
| 4 | 9.00565048878849 |
| 5 | 11.0046172791463 |
| 6 | 13.00390409145 |
| 7 | 15.0033820061521 |
| 8 | 17.0029832161817 |
| 9 | 19.0026686249351 |
| 10 | 21.0024140958786 |
These discrepancies may be related to correction values calculated in quantum electromagnetism, but this is unclear to the author at present.
Reference
[1] Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.
[2] Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.



Comments