*The painter ChatGPT “A visually striking representation of the Prisoner’s Dilemma.”
Can We Beat a Player Who Accurately Calculates Their Odds?
Let suppose that there is a player who can accurately measure his or her probability of winning from his or her hand and community cards, and manage risk consistently. This corresponds to the NPC that calculates probabilities using the Monte Carlo simulation shown in the previous post and determines the optimal bet amount accordingly. Currently, I am unable to beat players of this level, but is there any way to beat them? In fact, there is a strategy for this.
Since the optimal bet amount \(\small f\) is calculated for the estimated probability of winning \(\small p\), the optimal bet amount can be expressed as a function of the estimated probability of winning, as \(\small f=\pi(p)\). From the perspective of other players, the probability \(\small p\) estimated from the cards in hand is private information and cannot be known, but in fact the betting amount \(\small f\) is publicly available information with a certain degree of accuracy. Typically, this is expressed as how much you specify when you raise or bet, or how much you are willing to call. In other words, the estimated probability of winning \(\small p\) is private information, but the optimal bet amount \(\small f\) is public information that other players can know. In this case, if the function form of \(\small f=\pi(p)\) is known, it is possible to infer the strength of the player’s hand as:
\[ \small p^\ast = \pi^{-1}(f). \]
In this way, if you are able to know the behavioral patterns of your opponent, a strategy that uses those patterns to increase your chances of winning or increase your expected return is called an exploitative strategy. A strategy of accurately calculating the probability of winning and betting a fixed betting ratio \(\small f\) based on that may be the strongest strategy provided that an exploitative strategy is not used, but it may not be such a strong strategy in the sense that it is a strategy that makes it highly likely that the other player will be able to read your hand.
In games of incomplete information, the operation of inferring hidden information from public information is extremely important, and it is easy to understand that using such strategies in the real world can give you an advantage in competition with others. For example, in politics and the military, stealing hidden information or the results of decision-making from an enemy is called intelligence. Typically, this refers to the act of sending spies into an enemy organization or extracting information from traitors who are dissatisfied with the organization, but techniques such as exploitation strategies, which involve working backwards from publicly available information to infer an enemy’s hidden information and intentions (OSINT: Open Source Intelligence), also seem to be commonly used.
How to Guess Your Opponent’s Hand from Their Bets
An NPC that accurately calculates the probability of winning and makes betting decisions using the Kelly criterion or CRRA-type utility function will bet so that the bet ratio \(\small f\) given the probability of winning \(\small p\) is as close as possible to the following (when there are four players):
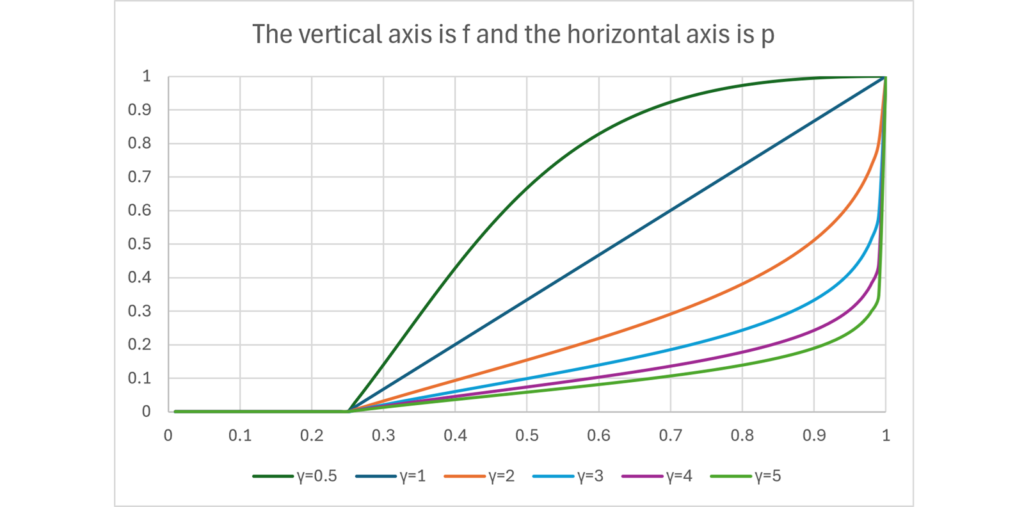
If we know the NPC’s level of risk aversion, we can determine the level of the estimated probability of winning \(\small p\). If your opponent’s estimated probability of winning is higher than yours, you should avoid raising your bet even if you have a strong hand. Conversely, even if your hand is not so good, you can be more aggressive if your opponent’s estimated probability of winning is lower.
Also, if you know the estimated probability of winning \(\small p\) for the opponent, you may be able to identify the cards your opponent is holding depending on the combination of cards. As an example, in a four-player game of Texas Hold’em, the exposed cards on the flop look like this:
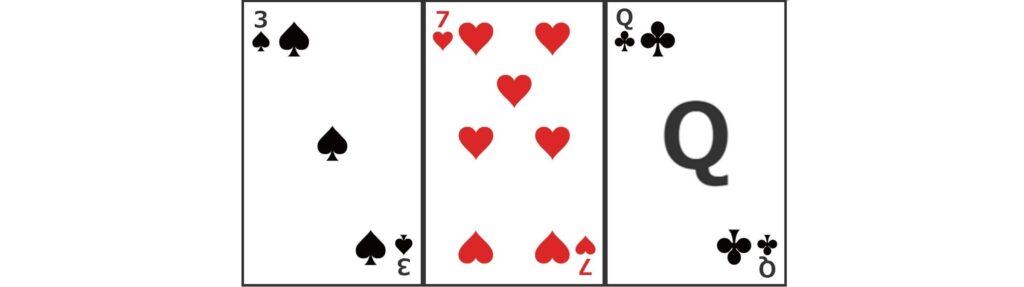
In this case, if the opposing player raises, it can be estimated that the opponent estimates his chances of winning to be about 50% (expected return: \(\small 4\times0.5-1=100\%\)). With these community cards, there is no possibility of a straight or flush, so if your opponent has a hand, it would likely be one pair, two pair, or three of a kind. However, with these community cards, even two pairs of 3 and 7 have a winning probability of nearly 65%, so we can assume that the hand is one pair. In addition, the winning rate of a pair at each rank is approximately 25% for a pair of 3s, 33% for a pair of 7s, and 53% for a pair of Qs. Therefore, we can infer that one of the cards in the raiser’s hand is a Q. We can also narrow down the range to the fact that the other card is any card other than 3, 7, or Q.
In this way, the range of combinations that narrows down the possible cards that your opponent may have based on their actions is called the range (just as it sounds). If you think your hand is stronger than this range, you can raise your bet and go for it, but if you think it is weak, you can decide to fold. By predicting an opponent’s hand in this way, you can accurately measure your own chances of winning, and it is not impossible to defeat a player (NPC) who manages risk consistently.
Counter Exploitation
A computer algorithm would never realize that its hand was being guessed, but a real person, with enough experience, would realize that perhaps their opponent was guessing their hidden hand from their actions. You may also be trying to guess your opponent’s intentions from their actions. If people were to realize this, I doubt many would allow themselves to continue to be exploited without taking any action. They may try to deceive their opponent by acting falsely so that they cannot guess their hand, or they may take measures such as introducing a random element to make it more difficult to predict.
Take political or military intelligence, for example, where you know that an adversary is stealing information about your country’s information and decision-making through espionage activities. In such cases, a strategy may be adopted in which false information is deliberately given to senior officials with access to such information, or different information is given to individual senior officials, in order to mislead enemy countries or identify spies or traitors. In addition, when a party believes that it has a strong means of inferring internal information about the party from publicly available information, it may deliberately present false public information in order to mislead the other party. This type of activity is called counter-intelligence.
Similarly, in Texas Hold’em, if a player believes that his or her betting strategy \(\small f=\pi(p)\) can be guessed by their opponent, they may offer a bet that is different from the strength of their hand in order to cause the opponent to make incorrect decisions or to prevent them from guessing their betting strategy. This strategy is called counter-exploitation. Typically, this includes bluffing, which involves betting more than you have, or slow playing, which involves appearing weaker than you have in order to encourage other players to increase their bets. Even if players do not use bluffing or slow play, they may incorporate an element of randomness into their betting strategy, offering different bets for the same hand strength in order to make it harder to guess.
When incorporating counter-exploitation into a betting strategy, players will adopt probabilistically different actions even if the estimated probability of winning \(\small p\) is the same. In this case, \(\small f\) in the betting strategy \(\small f = \pi(p)\) is not a scalar value, but a function that returns the probability distribution of the betting amount to be adopted. In game theory, a strategy that probabilistically selects multiple actions according to a probability distribution like this is called a mixed strategy. Conversely, a strategy that always takes the same action in the same situation is called a pure strategy. In games with incomplete information, such as Texas Hold’em, pure strategies are rarely optimal and mixed strategy solutions may need to be considered.
Texas Hold’em and Nash Equilibrium
He who fights with monsters should be careful lest he thereby become a monster. And if you gaze long enough into an abyss, the abyss will gaze back into you.
Friedrich Nietzsche, “Beyond Good and Evil”
I explained that you can predict your opponent’s hand from their betting strategy, and that by adopting a mixed strategy you can prevent your opponent from predicting your hand. You might think this is the perfect strategy. However, in reality your opponents may do the same, using mixed strategies to prevent you from predicting your hand, and their betting strategies may not be based solely on their own hand. Exploitation strategies and counter-exploitation will likely result in a cat-and-mouse game. If you come up with a counter to your opponent’s strategy, your opponent will come up with a different counter to that strategy. If that counter strategy fails, you’ll have to think of a different one. What does this repetition lead to?
Consider a betting strategy that takes into account the probability of winning with your own hand and the strength of your opponent’s hand as inferred from their bets. In this case, the optimal betting ratio \(\small f\) is a function of the winning probability of one’s own hand \(\small p_1\) and the winning probability \(\small p_2 = \pi_2^{-1}(f_2)\) estimated from the opponent’s bet \(\small f_2\), so it can be expressed as:
\[ \small f_1 = \pi_1(p_1, p_2) = \pi_1(p_1, \pi_2^{-1}(f_2)) = \pi_1(p_1, f_2). \]
However, if your opponent is also guessing your hand and considering a betting strategy, it should be represented as:
\[ \small f_2 = \pi_2(p_1, p_2) = \pi_2(p_2, \pi_1^{-1}(f_1)) = \pi_2(p_2, f_1). \]
In other words, since \(\small f_2\) is also a function of \(\small f_1\), when this is substituted into the equation for \(\small f_1\), it becomes
\[ \small f_1 = \pi_1(p_1, f_2) = \pi_1(p_1, \pi_2(p_2, f_1)) = \pi_1(f_1 \: | \:p_1,p_2). \]
In the same way, it can be also expressed as:
\[ \small f_2 = \pi_2(f_2 \: | \:p_1,p_2). \]
In an optimal strategy, if the \(\small f\) assigned to the argument and the \(\small f\) returned by the function are not the same value, then the player will incorrectly guess the opponent’s strategy, resulting in a contradiction. Therefore,
\[ \small \begin{align*} &f_1^\ast =\pi_1(f_1^\ast \: | \:p_1,p_2) = \pi_1(p_1, f_2^\ast) \\ &f_2^\ast =\pi_2(f_2^\ast \: | \:p_1,p_2) = \pi_2(p_2, f_1^\ast) \end{align*} \]
must hold in the optimal solution. In this way, the point where the argument and the return value of a function are the same is called the fixed point of the function. This means that the value remains the same no matter how many times the function is applied, and this is the point where
\[ \small f_1^\ast = \pi_1 \circ \pi_1 \circ \cdots \circ \pi_1 (f_1^\ast) \]
holds true. If we represent the betting strategies of two players as a set, and consider a function that takes that set as an argument and returns the betting strategies as a set, we can denote it as:
\[ \small \{f_1^{\ast}, f_2^{\ast} \} = \pi\left(\{f_1^{\ast}, f_2^{\ast} \}\: \Big| \: p_1,p_2 \right). \]
Such a function \(\small \pi\) is called a set-valued function. The optimal betting strategies of the two players can be expressed as fixed points of this set-valued function.
If the combinations of sets that players can adopt are finite and the strategy function \(\small \pi\) is a continuous function, the existence of this fixed point can be proven by a theorem of topology called Kakutani’s fixed point theorem. In game theory, a strategy expressed as this fixed point is called a Nash equilibrium strategy. It is known that a Nash equilibrium strategy in a zero-sum game is a Pareto optimal strategy in which one cannot improve one’s own gain (utility) any further unless someone voluntarily takes a loss, and in games such as Texas Hold’em in which cooperation with others is basically not possible, it is considered to be the final strategy. The optimal strategy in Texas Hold’em is the Nash equilibrium strategy, and playing with the Nash equilibrium strategy in mind is said to be a GTO (Game Theory Optimal) strategy.
In Texas Hold’em, each player is symmetric, so the optimal strategy can be found by calculating one’s own Nash equilibrium strategy, assuming that other players also adopt the same Nash equilibrium strategy as oneself. In reality, there are an astronomical number of possible combinations of cards and bets in Texas Hold’em, so it seems impossible to precisely calculate what a Nash equilibrium strategy would be. However, since the number of possible patterns is limited pre-flop, it appears that a mixed strategy to be adopted for each hand according to the Nash equilibrium strategy is calculated. As a result, it seems that 80 to 90 percent of professional games are decided pre-flop. As long as you’re excitedly waiting to open the cards to see if you’ll get a hand, you may still be an amateur.
Also, note that a Nash equilibrium strategy is not the optimal strategy against all opponents. This is a strategy that cannot be exploited against any opponent, but if you can read your opponent’s betting strategy (the opponent is adopting a strategy that deviates from the Nash equilibrium strategy), you may be able to increase your expected return by changing your strategy to match it. However, in order to do this, you need to collect some data about your opponents’ betting strategies and make some assumptions before you can do so. Except when playing with friends or in tournaments where famous players with distinctive playing styles gather, these conditions will rarely be met in typical situations.
Furthermore, mixed strategies based on Nash equilibrium can be a very painful decision-making method for humans. For example, if you hold AQo (different suits of A and Q), you would likely raise or call preflop, but a mixed strategy might mean you have to fold a certain percentage of the time to prevent your hand from being read. On the other hand, this means that there is a certain probability that you will have to make a strong raise (bluff) even if you have a weak hand. In this case, would you be able to choose to fold (raise) with a certain probability, even though you will likely end up losing a certain number of chips as a result? It is fair to point out that unless you are very determined, you may fall into a monotonous strategy of betting hard when you have strong hands and folding when you have weak hands.
In addition, the outcome of Texas Hold’em is heavily dependent on luck. By accurately calculating your winning rate and expected value and implementing a strategy, you may have to play a considerable number of times before you can see that you have become noticeably stronger. This means that the probability and expected value do not converge after 10 or 20 plays. It is unclear how many times this will be done, but it may require considerable mental strength to repeat a painful decision-making process in the belief that if the probabilities and expectations converge, it will be a superior strategy.
How to Incorporate Players’ Hand Guesses into the Game
This is getting long, so I will discuss this in another post, but what you can see is that deciding on a betting strategy in Texas Hold’em based on expected utility is a decision-making method used by beginner to intermediate level players, while advanced and above players are likely to make decisions in a completely different way. In order to consider players who are stronger than the player who maximizes expected utility, or NPCs with a range of strategies, it will be necessary to devise a decision-making algorithm that takes this into account.
Reference
[1] Acevedo, Michael, Modern Poker Theory: Building an Unbeatable Strategy Based on GTO Principles, D&B Publishing, 2019.


Comments