Introduction
This article explains how to handle the double-slit experiment in the Schrödinger equation. There are countless explanations of the double-slit experiment that do not use mathematics, but have you ever seen a text that uses mathematics to explain the calculations of the double-slit experiment using the Schrödinger equation? Of course, some of this does exist, but there are also many papers and websites that use incorrect calculations, and it can be quite difficult to find explanations that are derived through proper calculations.
In fact, in the early stages of my research into quantum mechanics, I was looking for a solution to the Schrödinger equation in the double-slit experiment, but I had a hard time finding one. After frustratingly searching Google, I found a question on an English message board site that asked, “How can you derive the calculation for the interference fringes in the double-slit experiment using the Schrödinger equation?” and I wanted to know more. The answer was that it was in Tomonaga’s “Quantum Mechanics, Vol 2.” Since the questions were in English and the respondents did not appear to be Japanese, I thought that everyone was probably struggling.
I was able to successfully obtain the Japanese version of Tomonaga Shin-ichiro’s “Quantum Mechanics II” and confirm the calculation results. I originally began my research with the idea of formulating quantum mechanics using the theory of Brownian motion, but the results of these calculations led me to realize that it was impossible to describe quantum motion using Brownian motion. This was the starting point of my research into quantum mechanics. So the purpose of this article is to introduce this. At the end, I will also briefly explain the interpretation of the double slit experiment that I introduce in my book.
Overview of the Double-Slit Experiment
Prosecutor: “There are two windows facing the front yard in that room. Through which window did the defendant break in? This is a very important point, so please answer clearly.”
Defendant’s answer to this question was very bizarre.
Defendant: “I entered the room through both windows at the same time.”
Shin-ichiro Tomonaga, “The Trial of the Photon”
The double slit experiment is said to be one of the most beautiful experiments in physics. As it is said, the experiment itself is very simple. However, the results are very puzzling. When an electron or photon is emitted into a space with two holes (slits), each time it is emitted it is detected as if it were a particle. On the other hand, if this is repeated multiple times, it is detected as a wavy probability distribution like the one shown below.
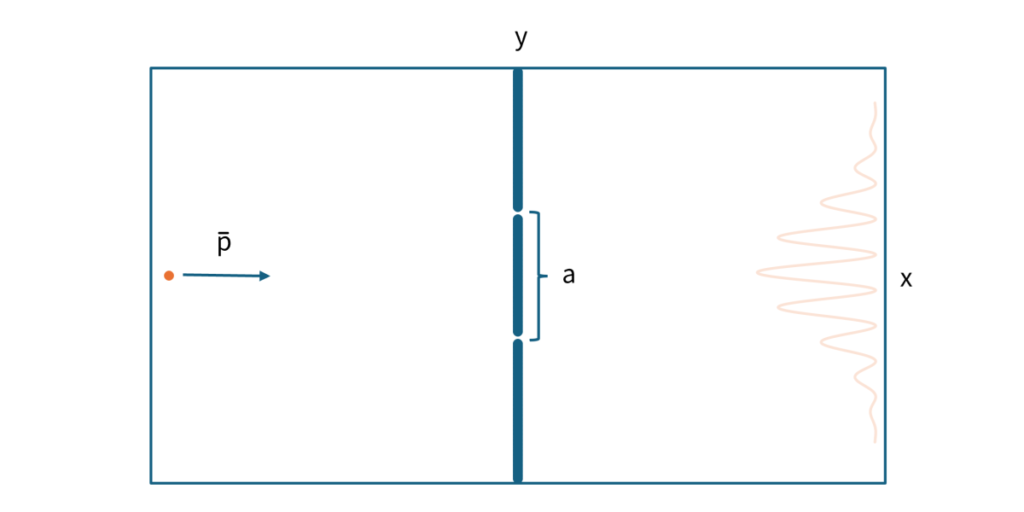
Here, \(\small a\) is the spacing between the slits, \(\small x,y\) are coordinate values with the center of the slit as the origin, and \(\small \bar{p}\) is the (average) momentum in the \(\small x\) axis direction. The double slit experiment is based on the idea that if the same experiment is performed with one of the slits blocked, the wave-like probability distribution disappears and becomes a random probability distribution that is close to normal distribution. Until around the 1960s, this was merely a thought experiment, but it seems that its correctness has been confirmed through actual experiments. The most famous experiment was conducted by Tonomura et al.[5] in the late 1980s.
You might think that there is no equation that can reproduce such results, but there is an equation that can reproduce these experimental results, even if only approximately, and this equation is the Schrödinger equation. However, when calculating the detection probability distribution in a double-slit experiment using the Schrödinger equation, the wave function when a quantum passes through the upper slit and the wave function when it passes through the lower slit must be combined. One implication of this is that in the double-slit experiment, even though the quantum is detected as if it were a single particle, it must be interpreted as passing through both slits simultaneously. Let us derive this result using the Schrödinger equation.
Mathematical Formulation
In order to obtain the probability distribution of quantum detection in the double-slit experiment, let us formulate it using the Schrödinger equation. Because there is a slit, one might wonder whether we should define this barrier as a potential function. However, in order to set the boundary condition (initial state) at the time of passing through the slit, the barrier is not defined as a potential function, and the Schrödinger equation in the free state is applied as is (For the Schrödinger equation in the free state, see
). That is, the fundamental equation is:
\[ \small i \hbar\frac{\partial \psi(x,y,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \left(\frac{\partial^2 \psi(x,y,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,t)}{\partial y^2} \right). \]
The boundary condition (initial state) is that the probability of passing through the upper and lower slits is \(\small 1/2\) respectively and is assumed as:
\[ \small \begin{align*} &\psi(x,y,0) = \frac{1}{\sqrt{2}}\psi_{+}(x,y,0)+\frac{1}{\sqrt{2}}\psi_{-}(x,y,0) \\ &\psi_{\pm}(x,y,0) = \frac{1}{\sqrt{\pi}\sigma} \exp\left(-\frac{x^2+(y\pm\frac{1}{2}a)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}x \right). \end{align*} \]
As in the free state, there is a certain uncertainty in the coordinates regardless of which slit it passes through, and the degree of uncertainty is expressed as \(\small \sigma\). By finding a solution based on the above fundamental equation and boundary condition, it is possible to derive the probability distribution of quantum detection in the double-slit experiment.
Before deriving the probability distribution for the double-slit experiment, we first determine the probability distribution for when it is determined which slit the quantum passes through. If one of the slits is blocked and it is revealed which slit the quantum passed through, the boundary condition will be one of
\[ \small \psi(x,y,0) = \psi_{\pm}(x,y,0). \]
However, since the fundamental equation and boundary condition in this case are the same as the Schrödinger equation in the free state,
\[ \small y(t) \sim N\left(\pm \frac{1}{2}a, \frac{\sigma^2}{2} + \frac{\hbar^2}{2m^2\sigma^2}t^2 \right) \]
is the solution, and nothing like interference fringes appears; it is detected as a random point following a normal distribution. Therefore, in order to produce interference fringes in the double-slit experiment, it would be impossible to tell which slit a quantum passed through.In other words, interference fringes will not appear unless a quantum passes through both slits at the same time. It will be clear that this is consistent with the explanation of the double-slit experiment given in the previous section.
Derivation of the Solution
As usual, let us find \(\small \psi(x,y,t)\) when the fundamental equation and boundary condition are:
\[ \small \begin{align*} & i \hbar\frac{\partial \psi(x,y,t)}{\partial t} = -\frac{1}{2} \frac{\hbar^2}{m} \left(\frac{\partial^2 \psi(x,y,t)}{\partial x^2}+\frac{\partial^2 \psi(x,y,t)}{\partial y^2} \right) \\ &\psi(x,y,0) = \frac{1}{\sqrt{2}}\psi_{+}(x,y,0)+\frac{1}{\sqrt{2}}\psi_{-}(x,y,0) \\ &\psi_{\pm}(x,y,0) = \frac{1}{\sqrt{\pi}\sigma} \exp\left(-\frac{x^2+(y\pm\frac{1}{2}a)^2}{2\sigma^2} \right)\exp\left(i\frac{\bar{p}}{\hbar}x \right). \end{align*} \]
However, in the double-slit experiment, a flat screen is used to detect the quanta, so the value on the \(\small x\) axis of the screen is expressed as \(\small X\) and the solution is found by putting \(\small \psi(X,y,t(X))\). We approximate
\[ \small x(t) \approx \frac{\bar{p}}{m}t \; \Rightarrow \; t(X) \approx \frac{mX}{\bar{p}} \]
by assuming that the expectation value \(\small \bar{p}\) of the momentum along the \(\small x\) axis is large enough that the uncertainty in the momentum \(\small \hbar/\sqrt{2}\sigma\) can be ignored. Since the problem itself is the same as the Schrödinger equation in the free state, the wave function in the \(\small y\) axis direction can be calculated as:
\[ \small \begin{align*} \psi_{\pm}(y,t)&= \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar t}{m\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{\hbar}x – \frac{\bar{p}^2 t}{2m \hbar} + \frac{\hbar t \left(y\pm\frac{a}{2}\right)^2}{2 m \sigma^4 \left(1 + \left( \frac{\hbar t}{m\sigma^2} \right)^2 \right)} \right\} \right). \end{align*} \]
Replacing \(\small t\) with \(\small X\) gives us
\[ \small \begin{align*} \psi_{\pm}(y,X)&= \frac{1}{\pi^{1/4}\sigma^{1/2}} \frac{1}{\left( 1+\frac{i \hbar X}{\bar{p}\sigma^2} \right)^{1/2}} \small \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(1 + \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 \right)} \right) \\ &\small \quad\;\times \exp \left(i \left\{ \frac{\bar{p}}{2\hbar}X + \frac{\hbar X \left(y\pm\frac{a}{2}\right)^2}{2\bar{p}\sigma^4 \left(1 + \left( \frac{\hbar X}{\bar{p}\sigma^2} \right)^2 \right)} \right\} \right). \end{align*} \]
To simplify the calculations, let us assume
\[ \small \frac{\hbar X}{\bar{p}\sigma^2} \gg 1. \]
This is an assumption that can generally be justified in double-slit experiments (meaning that X is taken to be very large; in fact, the distance from the slit to the screen is apparently several tens to several hundreds of meters). The constant part is difficult to calculate, so we will normalize it later. If we calculate only the exponential part, we can approximate it as:
\[ \small \begin{align*} \psi_{\pm}(y,X)& \propto \exp \left(- \frac{\left(y\pm\frac{a}{2}\right)^2}{2 \sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \times \exp \left(i\frac{\bar{p}}{2\hbar} \left\{X + \frac{\left(y\pm\frac{a}{2}\right)^2}{X} \right\} \right). \end{align*} \]
Since the wave function is
\[ \small \psi(y,X) = \frac{1}{\sqrt{2}}\psi_{+}(y,X) + \frac{1}{\sqrt{2}}\psi_{-}(y,X), \]
by calculating the probability distribution, we get
\[ \small \begin{align*} P(y,X) \propto & \;\exp \left(- \frac{\left(y+\frac{a}{2}\right)^2}{\sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) + \exp \left(- \frac{\left(y-\frac{a}{2}\right)^2}{\sigma^2 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \\ &+2\exp \left(- \frac{a^2}{4 \left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right)\exp \left(- \frac{y^2}{\left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \cos\left( \frac{\bar{p}}{\hbar}\frac{ay}{X}\right). \end{align*} \]
Because \(\small X\) is very large, we can ignore \(\small a\) inside exp and set \(\small a \rightarrow 0\) to obtain
\[ \small P(y,X) \propto 2\exp \left(- \frac{y^2}{\left(\frac{\hbar X}{\bar{p}\sigma^2} \right)^2 } \right) \left(1+\cos\left( \frac{\bar{p}}{\hbar}\frac{ay}{X}\right) \right). \]
This is the probability distribution of interference fringes in the double slit experiment. Incidentally, the wavy probability distribution shown in the first figure was calculated from this formula.
Interpretation of the Double-Slit Experiment
There are several interpretations of the double slit experiment. I would list them as follows (I am not familiar with each interpretation, so sorry if I make any mistakes).
- Probability interpretation (statistical interpretation, Copenhagen interpretation): The wave function represents the observation probability distribution of a quantum, and is detected by random sampling from that probability distribution when it reaches the screen. The observation probability distribution of a quantum is wavy, and accept it (as a principle or axiom) as a quantum has such a property (following the Schrödinger equation).
- Probability interpretation (quantum potential): The quantum is merely a particle, and it is interpreted as passing through one of the two slits to reach the screen. This is based on the theories of David Bohm and Edward Nelson. The wave-like observed distribution is due to the quantum having such a potential (pilot wave).
- Particle-wave duality (wave packet collapse) interpretation: Quantum behaves as a wave before being observed, and as a particle when observed. It is similar to the Copenhagen interpretation, but it seems to be more of a criticism of the Copenhagen interpretation. The idea that something acquires reality through observation. It is an interpretation similar to Einstein’s “The moon doesn’t exist when it’s not being observed” or Schrödinger’s cat.
- Many-worlds interpretation: The interpretation that the world branches out through observation, and that other worlds that are not observed in the probability distribution actually exist. A worldview in which an infinite number of deterministic worlds exist, and which world is selected is determined probabilistically. Proposed by Hugh Everett III.
- Subjective interpretation: The wave function collapses when quantum behavior is recognized as information by human consciousness. Is this a positive interpretation of Einstein’s criticism? It can be seen as an interpretation of self-help or spiritual quantum mechanics books. It is said that there is an originator (Eugene P. Wigner, who, although it may be surprising, is a leading physicist who won the Nobel Prize in Physics in 1963), but I am not sure whether it is true or not.
- Observation interferes with the past: The theory that the act of observation affects the past, so it is not possible to determine which slit it passed through. It is speculated that this is due to the fact that the phenomenon cannot be explained if we consider that time only moves in one direction in the double slit experiment. It is probably not Feynman’s own theory, but it seems to be an interpretation derived from Feynman’s path integral (the calculation of the path integral does not deny that quantum interference in the past).
The statistical interpretation (Copenhagen interpretation) and the particle-wave duality interpretation are often considered to be the same, but in this article I have decided to separate them. I suspect that this is probably what Max Born’s original interpretation was like.In addition, although the explanation I give below is in some ways an unconventional claim, it is an extension of statistical interpretation, and I have made the distinction because I want to say that it is, at least, an orthodox way of thinking. The change is that the reason why the quantum observation probability distribution is wavy is not accepted as a principle, but is sought in the nature of relativistic space-time. I will conclude by presenting my hypothetical interpretation of the double slit experiment.
The Double-Slit Experiment Is a Relativistic Phenomenon
One of the most amazing outcomes of Einstein’s special theory of relativity is that our familiar notion of time is fundamentally wrong. …… Time was assumed to be absolute, regular, and universal. No, said Einstein: time is flexible, stretchable and personal, so your time may be different from my time.
Simon L. Singh, ”Big Bang”
An implicit assumption in the interpretation presented in the previous section is that space and time are considered in Euclidean space (classical mechanical space). In other words, space is assumed to be three-dimensional Euclidean space \(\small R^3\) and time is assumed to be one-dimensional \(\small R\). This is thought to be due to the fact that the Schrödinger equation is derived by analogy with classical mechanics. However, in fact, the double-slit experiment also works for photons, and it is speculated that the phenomenon cannot be reproduced properly in electron experiments unless the electrons are fired at speeds close to the speed of light. In Tonomura’s experiments, electrons were fired at nearly 40% of the speed of light. The experimental result was that the probability distribution derived from the Schrödinger equation approximately reproduced the results.
An inference from this is that in order to understand the double-slit experiment one must base it on relativistic arguments. Even 40% of the speed of light is fast enough to break down classical mechanical theory, and photons naturally need to be considered in terms of the theory of relativity. And we can make the inference that none of the commonly offered interpretations of the double-slit experiment listed in the previous section are likely wrong, in the sense that they do not take this point into account. Furthermore, the fact that the probability distribution derived from the Schrödinger equation reproduces the results suggests that the Schrödinger equation is in fact an equation defined (albeit approximately) in relativistic space-time. The double-slit experiment is difficult to understand because it makes two seemingly contradictory claims:
- Schrodinger’s equation reproduces the results of the double-slit experiment.
- The Schrödinger equation is an equation defined for classical mechanical space-time.
My hypothesis is that the second claim is actually incorrect, which makes the double-slit experiment difficult to understand.
As I point out in my book and other posts, relativistic space-time is:
\[ \small x^2+y^2+z^2+c^2T^2=c^2t^2, \]
and if we assume time to be one-dimensional \(\small t\), then space must be treated as a three-dimensional sphere \(\small S^3\):
\[ \small S^3 = \{(x,y,z,s)|x^2+y^2+z^2+s^2=1\}. \]
However, we cannot know what the three-sphere looks like. This can be seen by analogy with the fact that when mapping the Earth, one wishes to map a two-dimensional sphere \(\small S^2\) onto a plane \(\small I \in R^2\) in two-dimensional Euclidean space, but this cannot be represented without stretching.
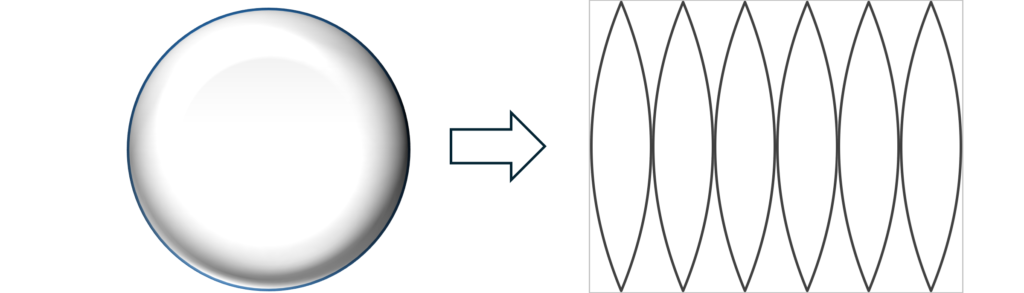
This means that a three-dimensional sphere cannot be represented in three-dimensional Euclidean space without the space expanding and contracting. If we treat time as one dimension, then we must think of space as expanding and contracting, which means that it is wrong to consider the double-slit experiment as a phenomenon in Euclidean space in the first place.
On the other hand, if we assume that space is a three-dimensional Euclidean space \(\small R^3\), we must consider two-dimensional time expressed by a complex function. That is, \(\small \zeta_{xyzt}\) satisfies
\[ \small \begin{align*} &x^2+y^2+z^2+c^2T^2=c^2\zeta_{xyzt}\zeta_{xyzt}^\ast \\ &\zeta_{xyzt} = \frac{1}{c}\sqrt{x^2+y^2+z^2}+iT = te^{i\theta_{xyzt}}, \end{align*} \]
which is defined as something different for each coordinate, represents the true nature of time. In this case, phenomena like the double-slit experiment would be interpreted as occurring as a result of time being stretched or contracted as applied to a moving quantum.
Also, while it may seem strange that a quantum particle can pass through two slits at the same time, the essence of a quantum particle is a probability distribution (noise), and it is assumed that it inherently has spatial extent. When it is detected, a point is sampled from that probability distribution, which can be thought of as producing a result similar to that of the double-slit experiment. In other words, the concepts of particles and waves are “models” (virtual concepts) created for the convenience of explaining phenomena that humans can observe, and are concepts that cannot be said to exist in reality. One of the reasons why many cult interpretations have arisen is that the concepts of particles and waves, which are merely models, are mistaken for real things.
This is my interpretation of the double slit experiment. If we assume that my theory is correct, then in order to theoretically understand the double-slit experiment, we need the theories of relativistic quantum mechanics (quantum field theory) and quantum electromagnetism. In the first place, undergraduate level knowledge of quantum mechanics is insufficient, and it would be impossible to understand without graduate school level knowledge of quantum mechanics (although even then it may be impossible). It’s worth pointing out that it might be best not to attempt this in the naive hope that some undergraduate level knowledge of quantum mechanics will lead to the right conclusions.
Reference
[1] Tomonaga, Shin-ichiro (1962). Quantum Mechanics Volume 1:Old Quantum Theory. North-Holland.
[2] Tomonaga, Shin-ichiro (1966). Quantum Mechanics Volume 2:New Quantum Theory. John Wiley & Sons (Interscience Publishing).
[3] Hirano, Kaname (2022), Quantum Mechanics with Multi-Time Theory, Amazon Kindle Store.
[4] Hirano, Kaname (2024), Complex Functions and Schrödinger Equation, Amazon Kindle Store.
[5] Tonomura, Akira et al (1989), Demonstration of Single‐electron Buildup of an Interference Pattern. American Journal of Physics, 57, 117-120.
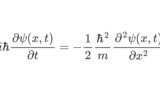


Comments