Overview
Since I have started developing a mobile game, we have been a little behind in considering the algorithm of the Texas Hold’em AI, but we have now got a rough idea of what to do pre-flop, so this time we will summarize the general guidelines for considering a behavioral model on the flop.
Hole and Community Card Abstraction
After the flop, the number of combinations of hole cards and community cards increases dramatically, so it is not realistic to consider a strategy for each combination of cards as you can before the flop. Therefore, we consider a model that calculates the equity (approximately, probability of winning) that can be inferred from the hand and community cards, and changes the strategy adopted depending on that equity. To be more precise, we should guess the opponent’s hand range (using Bayesian estimation based on play history or assuming a GTO strategy) and calculate the equity based on that hand range, but since the game I’m considering is one in which the goal is for the player to win, there’s no need for the NPC to be that strong. Therefore, it would be best to simply calculate equity assuming Any Hand (if I try it and it seems unreasonable, I will consider calculating it assuming something like a pseudo-GTO).
Reflecting Player Preferences
To reflect the player’s irrational preferences in their behavior, we express them by biasing the equity calculated above. This bias is presumably influenced by the following factors:
- Hole Cards: If you have a pocket pair or A, K, you can be aggressive even with high cards, etc.
- Hands you can make with your hand and community cards: Becoming aggressive with a flush or flush draw, being aggressive with a straight or straight draw, being too cautious with top pair, etc.
For 1, we can simply inherit and use the pre-flop model parameters. For 2, it may be better to inherit the pre-flop model parameters and introduce flop-specific parameters (to bias by hand, flush draw, straight draw, backdoor, etc.).
Equity Probability Distribution
I wrote that equity is the evaluation criterion when considering a model of player behavior on the flop, but in reality it is a competition with the strength of the hand held by the opponent, so even if your hand is in the top 10% of hands, if your opponent has an even stronger hand, you are likely to lose. In other words, the relative ranking of equity is more important as a measure of hand strength than the absolute level of equity. To make matters worse, equity is not a uniform probability distribution. In other words, if your equity (probability of winning) is, say, 90%, it doesn’t mean that you have the best 10% of hands.
Specifically, if we calculate the probability distribution of equity on the flop for each number of players, we get the following probability distribution. This is estimated by generating a simulation of the common card states in the hand and on the flop, and then performing further simulations to calculate the probability of winning (Simulation in Simulation). This is a method that takes a very long time to calculate, requiring nearly 100 million simulation calculations (10,000 times x 10,000 times), which ended up taking nearly half a day to run the calculations on a PC.
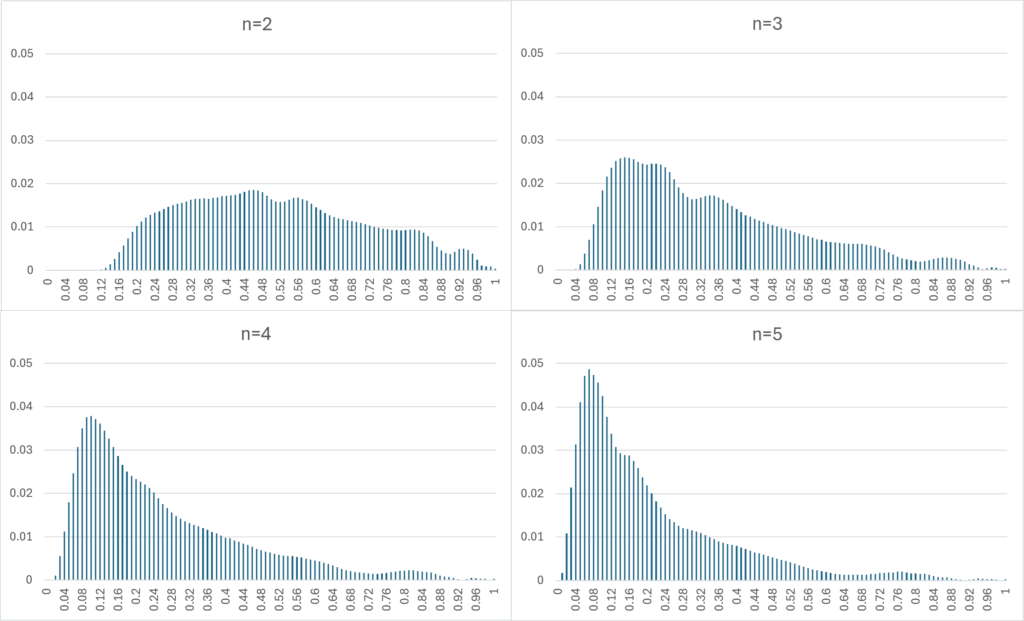
For example, if your equity (chance of winning) is 90% in a two-player game, that means you’re in the top 3% or so, and your hand may seem stronger than its apparent chance of winning. This tends to decrease as the number of players increases, and if there are five players, even an equity of around 67% will put you in the top 3%. In this case, we must consider the two situations:
- 90% equity with 2 players
- 67% equity with 5 players
to be equally bullish. When considering strategy on the flop, you need to consider this in appropriate terms.
How to Convert Equity into a Score
Suppose that in a given situation, you can estimate your equity to be \(\small p\). Let the probability density function of equity be \(\small \phi(p)\) and the probability distribution function be \(\small \Phi(p)\). Then,
\[ \small \Phi(p) = \int_0^p\phi(z)dz \]
holds. \(\small \phi(p)\) represents the probability distribution function illustrated in the previous section. To convert equity into the strength of the hand, we call \(\small s = \Phi(p)\) the score. If we calculate the probability distribution that the score \(\small s\) follows from a combination of random hand and community cards, we can see that it results in a uniform distribution \(\small U[0, 1]\). By determining the behavior of NPCs based on numerical values that follow this uniform distribution, it is possible to treat behavioral standards in a variety of situations in a unified manner.
In Texas Hold’em, the probability of getting a hand and the relative strength of the completed hand change depending on the number of players and the betting rounds (Flop, Turn, River). However, by converting the scores into a uniformly distributed score using the method described above and determining actions (raise, call, fold) based on that score, we can create a behavioral model that is somewhat consistent.
Other Conditions
In addition to the hole and common cards, the following information needs to be treated as a state that can change behavior.
- Whether you are the aggressor (if you receive a donk bet, you are considered a non-aggressor)
- Position (IP or OOP)
- Number of remaining players
- Stack Pot Ratio (SPR)
We will consider how to handle this information when we consider the detailed specifications of the player behavior model on the flop.
Simplifying Action Options
The amount of chips to bet or raise can be any amount as long as it is greater than the minimum raise amount. However, since it is mathematically not easy to handle continuous numerical decision-making in reality, it is better to discretize the options available for decision-making. Even if you could specify any number in an actual game, it would only make it difficult to operate, so it would be more realistic to narrow down the options in the game’s UI. Specifically, it might be good to be able to select the following numbers:
Bet: 0 (Check), 1/12, 1/6, 1/4, 1/3, 1/2, 2/3, 3/4, 1, 1.5, 2, 3, all-in in the pot
Raise: 0 (Fold), 1 (Call), 2, 2.5, 3, 3.5, 4, 5, 6, 9, 12, 16, all -in
Note that these are all numbers that represent multipliers. It would be sufficient to specify a multiplier equivalent to two raises in one go. If the stack is 100bb, and the bet is 3bb, an all-in would be 33x, so it doesn’t seem like there would be any big losses.
Turn, River Extensions, and Other Extensions
We have considered this as a model of player behavior on the flop, but the only difference is the probability distribution when converting equity into a score on the turn and river; basically, the same approach can be adopted. All that’s left is to define parameters such as decision-making habits on the turn and river (being cautious on the turn, increasing the proportion of bluffs on the river, etc.), and you’ll be able to define a complete model of player behavior. From next time onwards, I would like to delve deeper into player behavior models on the flop, turn, and river in the following order.
- Refining the Flop Behavior Model
- Detailed behavioral model for turn and river
- Try implementing it and make corrections if there are any areas that need refinement.
- Prototype implementation
Furthermore, because the approach in this article is based on equity, it can be applied to games other than Texas Hold’em in a fairly similar way. It is also possible to apply this to Short Deck Hold’em and Omaha Hold’em, so if it can reproduce human-like play to a certain extent, it is expected to become a behavioral model that can be applied to games with different rules.



Comments