Optimal Preflop All-In
I feel like I’ve made a strange post once, but following on from last time, let’s consider the application of counterfactual regret minimization. Consider Texas Hold’em (heads-up) with only two players. When there are two players, the Nash equilibrium strategy is uniquely determined (because the strategies adopted by the two players can be symmetrical), so one might think that the challenge is how well the GTO strategy has been mastered, and that this is the type of game in which skill differences are most evident. In fact, challenging an opponent to a heads-up match is like saying, “You’re probably worse than me anyway,” and can sometimes be perceived as picking a fight.
However, even if you think you cannot win due to the difference in skill level in reality, with some ingenuity you can turn heads-up into just a game of luck. In other words, if you give your opponent the choice between going all-in or folding pre-flop, they will also have no choice but to choose between going all-in (calling) or folding. In other words, if you make the right preflop all-in hand choices, you can make a heads-up match even (though of course you can’t win if both players are using the optimal strategy). When the stack is deep, it can be difficult to use this strategy because your opponent will likely just fold if they are not willing to go all-in, but if the stack is around 50bb or less, settling the game with a pre-flop all-in may be a realistic strategy (this type of strategy is called push or fold). The purpose of this article is to find the optimal heads-up all-in strategy using counterfactual regret minimalization, which was explained last time.
Assuming that both players have only the option of going all-in or folding, here is the payoff table for the options and outcomes for SB and BB:
| SB | BB | |
|---|---|---|
| SB folds | -0.5bb – Ante | 0.5bb + Ante |
| SB all-in, BB fold | 1bb + Ante | -1bb – Ante |
| SB,BB all in, SB wins | +Stack | -Stack |
| SB,BB all in, BB wins | -Stack | +Stack |
| SB,BB all in, chop | 0 | 0 |
One factor that influences this problem is the stack size, because the blinds paid by the SB and BB are different, which causes the hand ranges that the SB and BB should use to be different. It can be inferred that the larger the stack, the narrower the all-in range will be, since the profit and loss from folding will be relatively smaller compared to the profit and loss from going all in. Therefore, let’s look at some specific hand ranges for several stacks.
The specific calculation algorithm is as follows. Note that because the optimal strategies for SB and BB are different, the counterfactual regret needs to be calculated for each position.
- Two players randomly draw two hands \(\small h_{SB},h_{BB}\). Here, let \(\small h_{SB},h_{BB}\) represent the 169 possible hands (it is not necessary to calculate with 1326 possible card combinations).
- Determine the SB’s action (all-in or fold) according to the strategy function table \(\small \pi_{\text{SB}}[h_{SB}]\). If SB folds, calculate payoff and proceed to step 5.
- If the SB chooses all-in, the BB’s action (all-in or fold) is determined according to the strategy function table \(\small \pi_{\text{BB}}[h_{BB}]\).
- If the BB goes all-in, five community cards are drawn randomly to determine the winner. Calculate the payoff \(\small r_{\text{mixed},k},k \in{\text{SB},\text{BB}}\) from the determined hands and actions of the two players.
- Calculate each player’s regret using the following formula and add it to the total (to be calculated separately for each position).
\[ \small \begin{align*} &R_{\text{all-in},k}(h) = \frac{1}{T} \sum_{t=1}^Tr_{\text{all-in},k}(h, t)-r_{\text{mixed},k}(h, t) \\ &R_{\text{fold},k}(h) = \frac{1}{T} \sum_{t=1}^Tr_{\text{fold},k}(h, t)-r_{\text{mixed},k}(h, t), \;k \in\{\text{SB},\text{BB}\} \end{align*} \]
\(\small r_{\text{all-in},k},r_{\text{fold},k}\) are the payoffs for choosing all-in and for choosing to fold, regardless of the decision made by the strategy function. Actions that match the strategy function result in zero payoffs, but actions that differ from the strategy function result in different payoffs. The probability of selecting all-in or fold corresponding to the hand is updated based on the calculated regrets. - Steps 1 to 5 are repeated for the number of simulations to determine the optimal strategy function.
Below are links to the tools that were actually developed.
It has been extended to allow the setting of the rake and the specification of the \(\small \gamma\) value of the power function:
\[ \small U(s) = s^{1-\gamma} \]
as the objective function. The convergence of the simulation is very poor, and at least one million calculations are required, and if possible, around 10 million calculations. It takes 5 to 10 minutes to calculate 10 million times, so if you want to do the calculation, it’s best to do it when you don’t mind your PC being occupied for a while. That being said, I don’t think there are any readers who are so curious as to calculate it themselves, so I’ve prepared a page where you can see the results of the calculations in advance.
Since this will likely be used in tournaments, I’ve done detailed calculations for stacks between 2 and 20bb. I’ve also done calculations for ante sizes of 0.125bb and 0.25bb. You can refer to these as needed. Let’s take a look at the results of the specific calculations.
Calculation Result
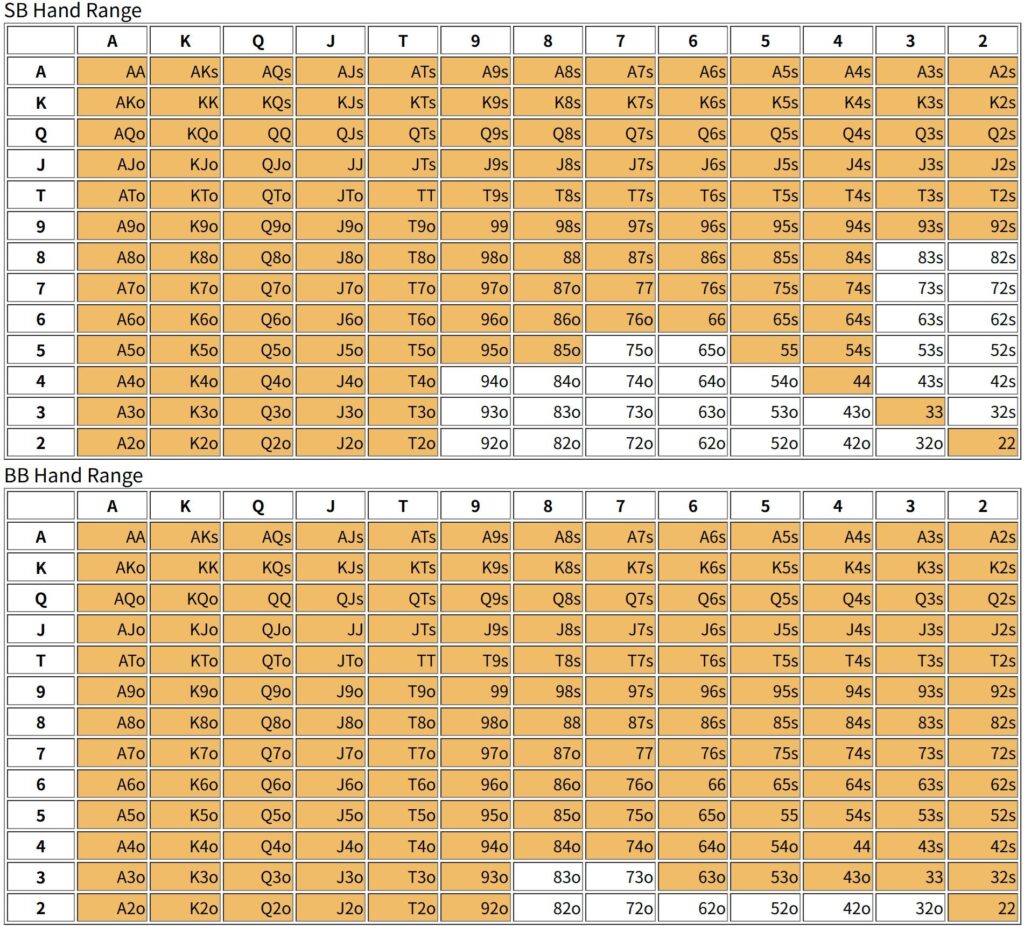
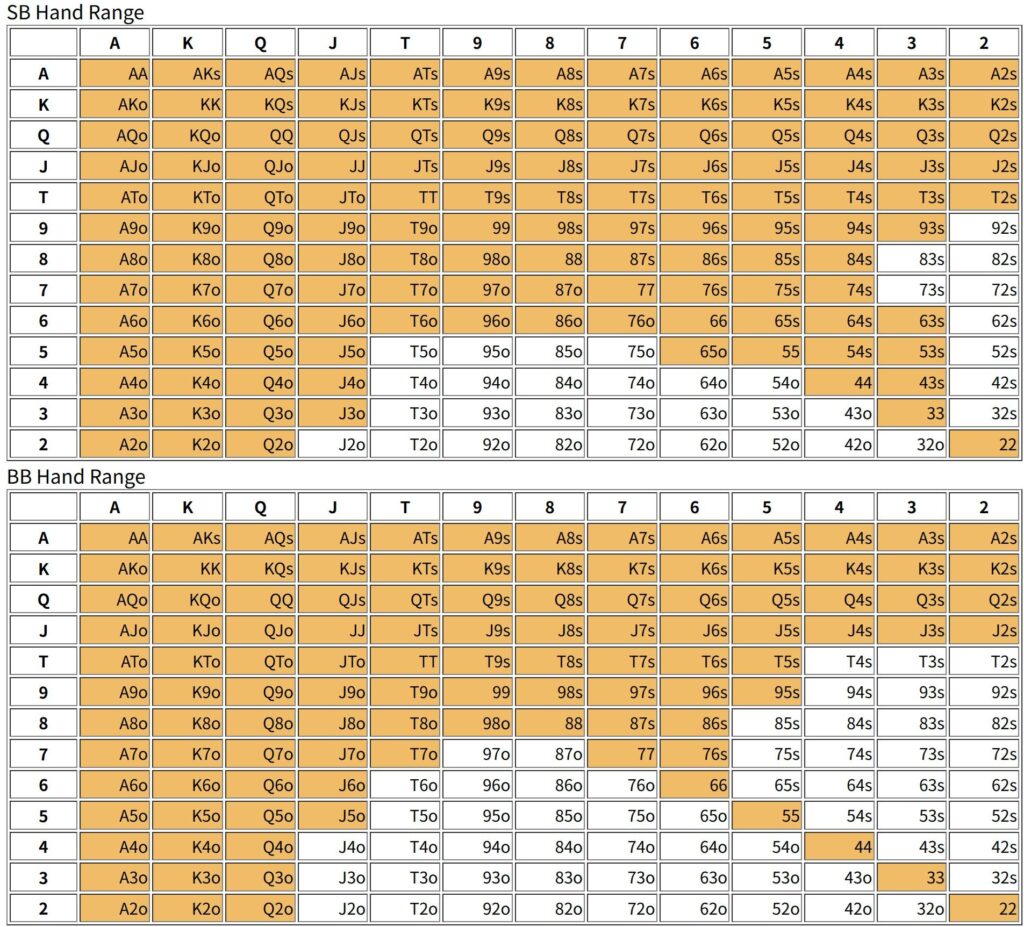
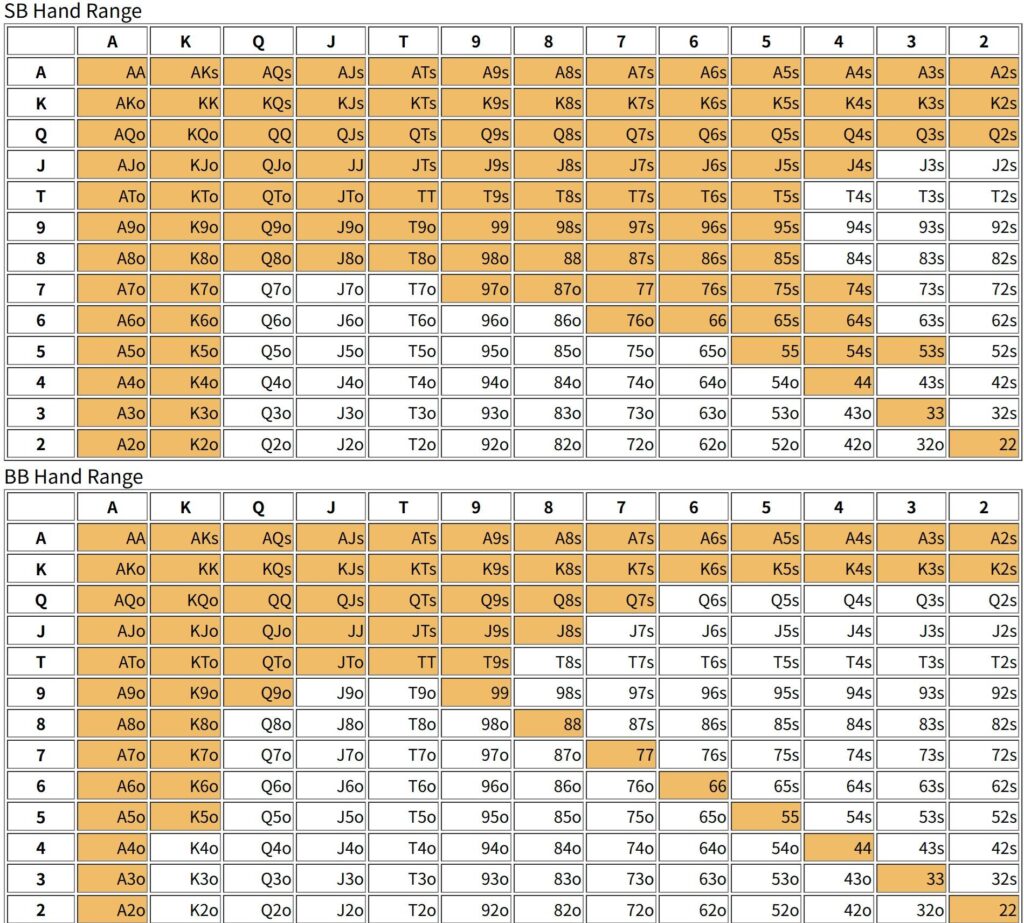
Let’s consider some conditions. Specifically, the hand ranges for stacks of 3bb, 5bb, 10bb, and 50bb are as follows:
[3bb]
[5bb]
[10bb]
[50bb]
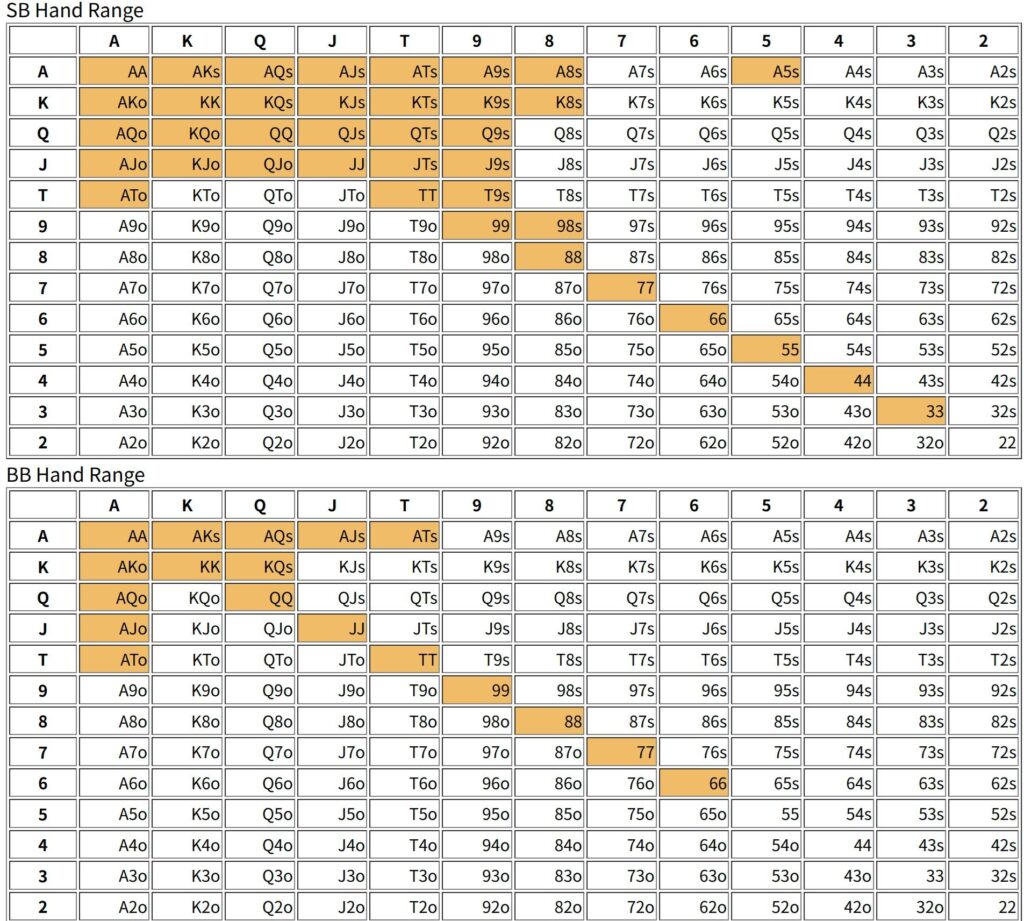
It may seem odd, but the SB generally has a wider hand range, probably because there is an element of bluffing involved, since the BB might fold. However, since the blind burden is heavier on the BB, the BB should have a wider hand range. This tendency can be observed when the stack gets smaller, and the hand range width is reversed when the stack is around 5bb.
Another important tendency is that the SB’s hand range tends to include more suited and connected hands. With a decent stack, this means the SB needs to include some speculative hands to include bluffing. The BB tends to choose a hand range that is biased towards pocket pairs, Axs, and Kxs. Since the BB is the second player, he will choose a hand that is suitable for defense. Thinking about it this way, hand ranges may change depending on the position as well as the player’s preferences. We will consider this further in the future.
Conclusion and Further Extension
You may be wondering if there is a further extension, but I would like to consider an extension for three or more players. In this case, the hand range will change depending on whether the player in front goes all-in or folds. For example, in a four-player game, the BTN will decide whether the CO goes all-in or folds, and the SB will have to consider strategies for four different combinations. Also, when playing with three or more players, there are an infinite number of Nash equilibria, so the optimal strategy will vary depending on the opponents’ hand ranges. However, it is possible to calculate the hand range calculated using CFR, and it is expected that the range will be relatively balanced, so let’s try calculating it, even though it may take some time.
Another game I’m thinking of is one in which you can play Texas Hold’em against an AI, but a game where the options are limited to all-in or folding could also be interesting. By playing the actual game while looking at the recommendations for the best choices, you might be able to see whether you should go all-in in different situations. I’ll try to implement this in the future.




Comments