Introduction
In the previous post:
we showed that the orbits of planets and other objects around stars are elliptical orbits and that their equation of motion is:
\[ \small \begin{align*} &r(t) = \frac{a(1-\epsilon^2)}{1+\epsilon \cos \omega(t)} \\ &x(t) = r(t)\cos \omega(t) \\ &y(t) = r(t)\sin \omega(t) \\ &z(t) = 0 \\ &\frac{d\omega}{dt} = \frac{|L|}{mr^2}. \end{align*} \]
Here, \(\small a\) is the major radius, \(\small \epsilon\) is the eccentricity, and
\[ \small |L| = \sqrt{L^2} = \sqrt{Gm^2Ma(1-\epsilon^2)} \]
is the orbital angular momentum. Unlike uniform circular motion, \(\small \omega(t)\) cannot have a constant speed but must satisfy the differential equation:
\[ \small \frac{d\omega}{dt} = \frac{|L|}{mr^2} = \sqrt{GM}\frac{(1+\epsilon \cos \omega(t))^2}{a^{3/2}(1-\epsilon^2)^{3/2}}. \]
The problem addressed in this article is to find a solution to this differential equation and accurately determine the elliptical orbit with respect to time.
Kepler Equation
Instead of solving a differential equation, let us consider a way to find the solution by solving an algebraic equation called the Kepler equation. To explain this, we need to explain some complicated concepts, but the simplest way to explain it is as shown in the figure below.
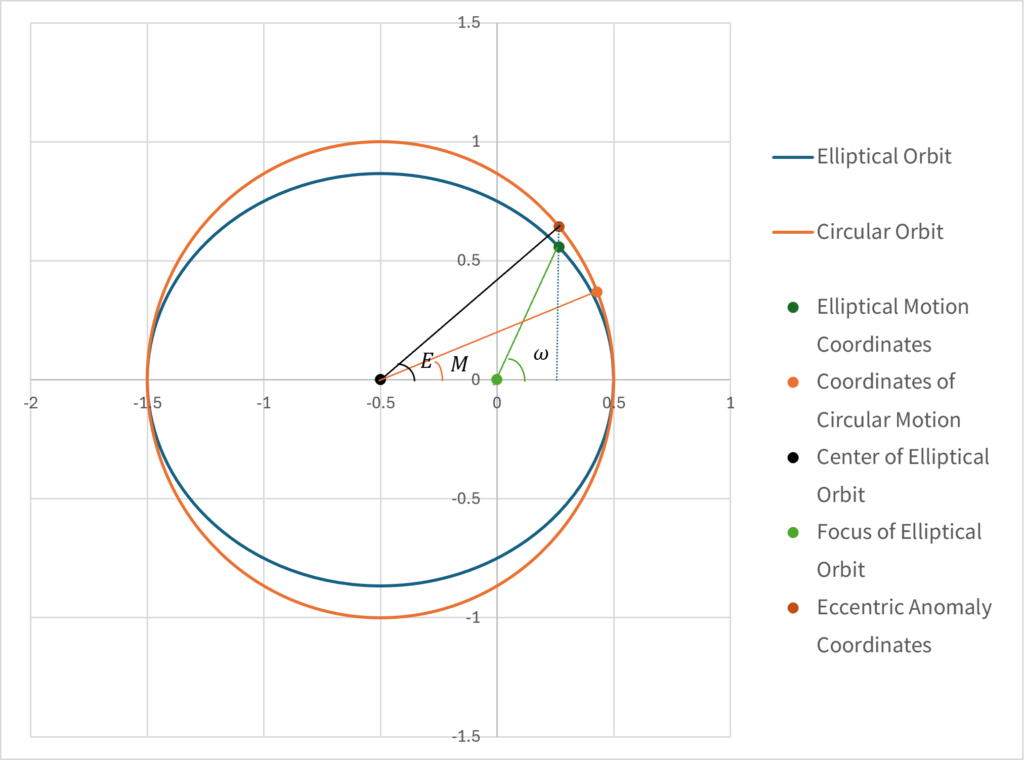
The value written as \(\small \omega(t)\) is a parameter that represents the angle between the focus of elliptical motion and the coordinates relative to the \(\small x\)-axis, and is called the true anomaly. Instead of the focus, we can also define the center and coordinates of the elliptical motion, and the angle \(\small E(t)\) that the coordinates obtained by extending the \(\small y\)-axis of the elliptical motion in a straight line into a circular motion make with the \(\small x\)-axis, and this is called the eccentric anomaly. As a comparison with elliptical motion, consider uniform circular motion with the same period \(\small T\), and the angle \(\small M(t)\) that the center of the elliptical motion and the coordinates of that uniform circular motion make with the \(\small x\)-axis is called the mean anomaly. By definition, it can be expressed as:
\[ \small M(t) = 2\pi\frac{t}{T}. \]
Note that \(\small \omega(t)\) is the angle relative to the coordinates in elliptical orbits, while \(\small E(t),M(t)\) is the angle relative to the coordinates in circular orbits.
Find the relationship between each angle and the orbital radius. Since the areal velocity of both elliptical motion and uniform circular motion is constant, the ratio of the area swept up to time \(\small t\) to the area enclosed by the orbit must be the same. In addition, the ratio of the area of the sector of the ellipse formed by the angle \(\small \omega(t)\) to the area of the sector of the circle formed by the coordinates of the eccentric anomaly must be the same value. In other words,
\[ \small \frac{M(t)}{2\pi} = \frac{\Delta d}{\pi a b} = \frac{\Delta c}{\pi a^2} \]
holds if the area of the sector enclosed by the focus, the \(\small x\)-axis, the coordinates of the elliptical motion, and the coordinates of the eccentric anomaly are \(\small \Delta d, \Delta c\), respectively. Here, \(\small b=a\sqrt{1-\epsilon^2}\) represents the minor radius of the ellipse.
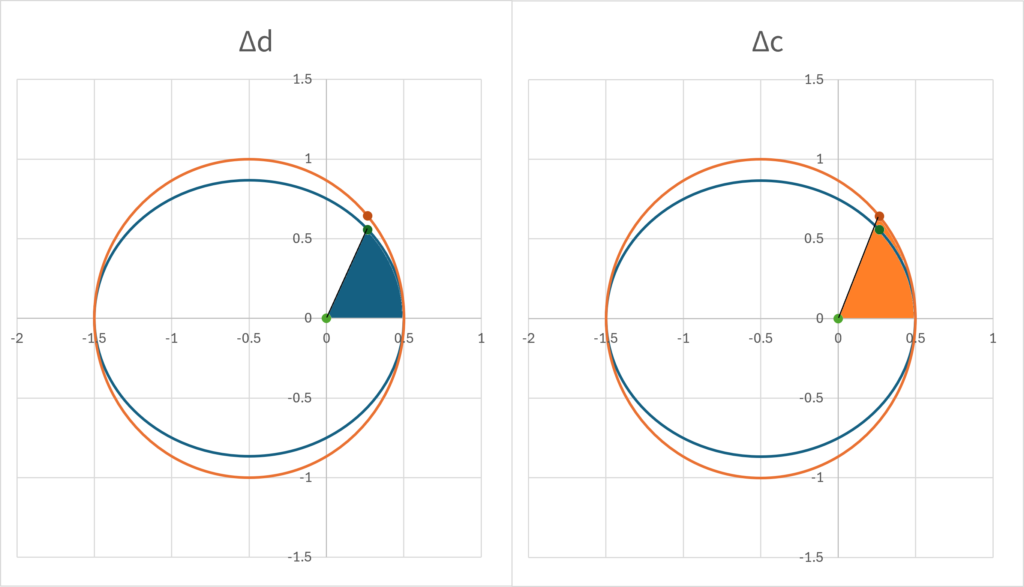
To find \(\small \Delta c\), subtract the area of the triangle enclosed by the center, focus, and eccentric anomaly from the area of the sector enclosed by the center, the \(\small x\)-axis, and the coordinates of the eccentric anomaly. Since the area of a sector is the area of a circle, \(\small \pi a^2\), multiplied by the central angle, we get
\[ \small \Delta c_1 = \frac{1}{2}a^2E(t). \]
The distance between the center and the focus is \(\small a\epsilon\) and the vertical length is \(\small a\sin E(t)\), so the area of the triangle is:
\[ \small \Delta c_2 = \frac{1}{2}(a\epsilon) a\sin E(t). \]
Therefore,
\[ \small M(t) = E(t)-\epsilon\sin E(t) \]
can be obtained. This equation is an algebraic equation called the Kepler equation.

In addition, the coordinates of an elliptical orbit can be expressed as:
\[ \small x(t)= a\cos E(t)-a\epsilon, \quad y(t) = a\sqrt{1-\epsilon^2} \sin E(t) \]
using the eccentric anomaly \(\small E(t)\). This can be confirmed by noting that the distance between the focus and the center is \(\small a\epsilon\) and that the minor radius of the elliptical orbit is \(\small b=a\sqrt{1-\epsilon^2}\). Hence,
\[ \small r(t) = \sqrt{x^2(t)+y^2(t)} = a(1-\epsilon\cos E(t)) \]
can be obtained. Since
\[ \small r(t) = \frac{a(1-\epsilon^2)}{1+\epsilon \cos \omega(t)} = a(1-\epsilon\cos E(t)) \]
holds by this equation, the relationship between \(\small \omega(t)\) and \(\small E(t)\) can be obtained as:
\[ \small \sin E(t) = \frac{\sqrt{1-\epsilon^2}\sin \omega(t)}{1+\epsilon \cos \omega(t)} \\ \small \sin \omega(t) = \frac{\sqrt{1-\epsilon^2}\sin E(t)}{1-\epsilon \cos E(t)}. \]
Solution using Bessel Functions
Let us consider how to solve Kepler’s equations:
\[ \small M(t) = E(t)-\epsilon\sin E(t) \]
for \(\small E(t)\) as a function of \(\small M(t)\) (i.e., a function of \(\small t\)). Since \(\small M(t)-E(t)\) has a period of \(\small 2\pi\), we can use a Fourier transform with a sine series to obtain
\[ \small E(t)-M(t) = \sum_{i=n}^\infty B_n \sin n M(t). \]
When the Fourier coefficients are subjected to the inverse Fourier transform,
\[ \small B_n = \frac{2}{\pi} \int_0^\pi (E(t)-M(t)) \sin n M(t) dM(t) \]
holds. By integrating by parts, we get
\[ \small B_n = \frac{2}{\pi}\left(\left[ -(E(t)-M(t))\frac{\cos nM(t)}{n} \right]_{M(t)=0}^{M(t)=\pi}+\int_0^\pi \frac{\cos nM(t)}{n}(dE(t)- dM(t))\right). \]
The first term is 0, and
\[ \small \int_0^\pi \frac{\cos nM(t)}{n}dM(t) = 0 \]
holds. Therefore,
\[ \small \begin{align*} B_n &= \frac{2}{\pi n} \int_0^\pi \cos nM(t) dE(t) \\ &= \frac{2}{\pi n} \int_0^\pi \cos n(E(t)-\epsilon\sin E(t)) dE(t) \ \end{align*} \]
can be obtained. By substituting \(\small x=n\epsilon\) and comparing with the Bessel integral formula:
\[ \small J_n(x) = \frac{1}{\pi}\int_0^{\pi} \cos(n\theta-x\sin\theta)d\theta, \]
we can obtain
\[ \small B_n = \frac{2}{n}J_n(n\epsilon). \]
Substituting into the sine series equation,
\[ \small E(t) = M(t)+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin nM(t) \]
is the solution to the Kepler equation. Since the orbital radius is:
\[ \small r(t) = a(1-\epsilon\cos E(t)), \]
we get
\[ \small r(t) = a-a\epsilon \cos\left(M(t)+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin nM(t) \right). \]
\(\small \omega(t)\) can be found by calculating backwards from
\[ \small \cos \omega(t) = \frac{1}{\epsilon}\left(\frac{a(1-\epsilon^2)}{r(t)}-1\right). \]
Note that since \(\small \cos^{-1}(x)\) is a multi-valued function, it is necessary to choose an appropriate principal value. The \(\small \omega(t)\) calculated in this way is the solution to differential equation:
\[ \small \frac{d\omega}{dt} = \frac{|L|}{mr^2} = \sqrt{GM}\frac{(1+\epsilon \cos \omega(t))^2}{a^{3/2}(1-\epsilon^2)^{3/2}}. \]
Let the period be \(\small T=1\) and denote it as:
\[ \small E(t) = 2\pi t+2\sum_{i=n}^\infty \frac{J_n(n\epsilon)}{n} \sin 2\pi nt. \]
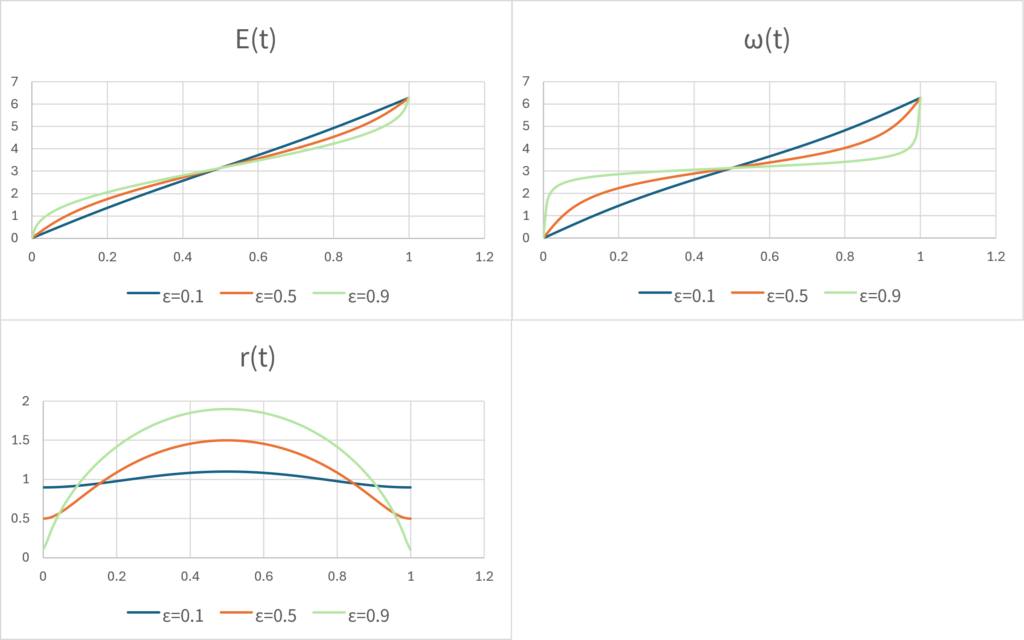
For some \(\small 0<\epsilon<1\), the graphs of \(\small E(t),r(t),\omega(t)\) in this case are shown below.
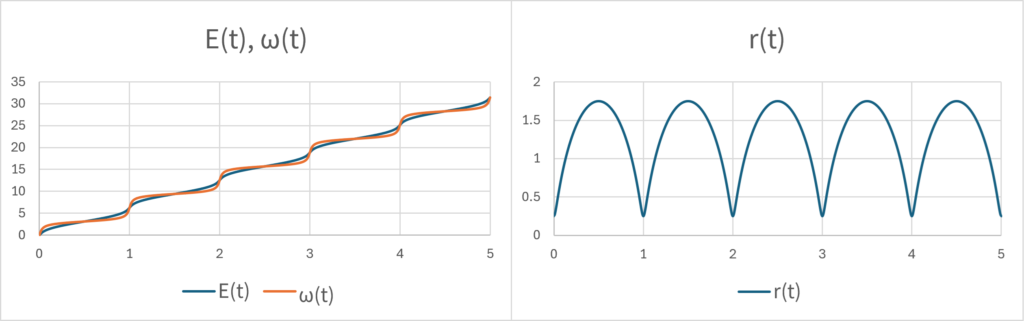
These variables behave periodic, and if we connect them and graph them from \(\small t>1\) onwards, we get the following graphs. It is easy to see that \(\small E(t),\omega(t)\) is a monotonically increasing function with respect to \(\small t\), and that \(\small \omega(t)\) seems to satisfy the differential equation shown at the beginning.
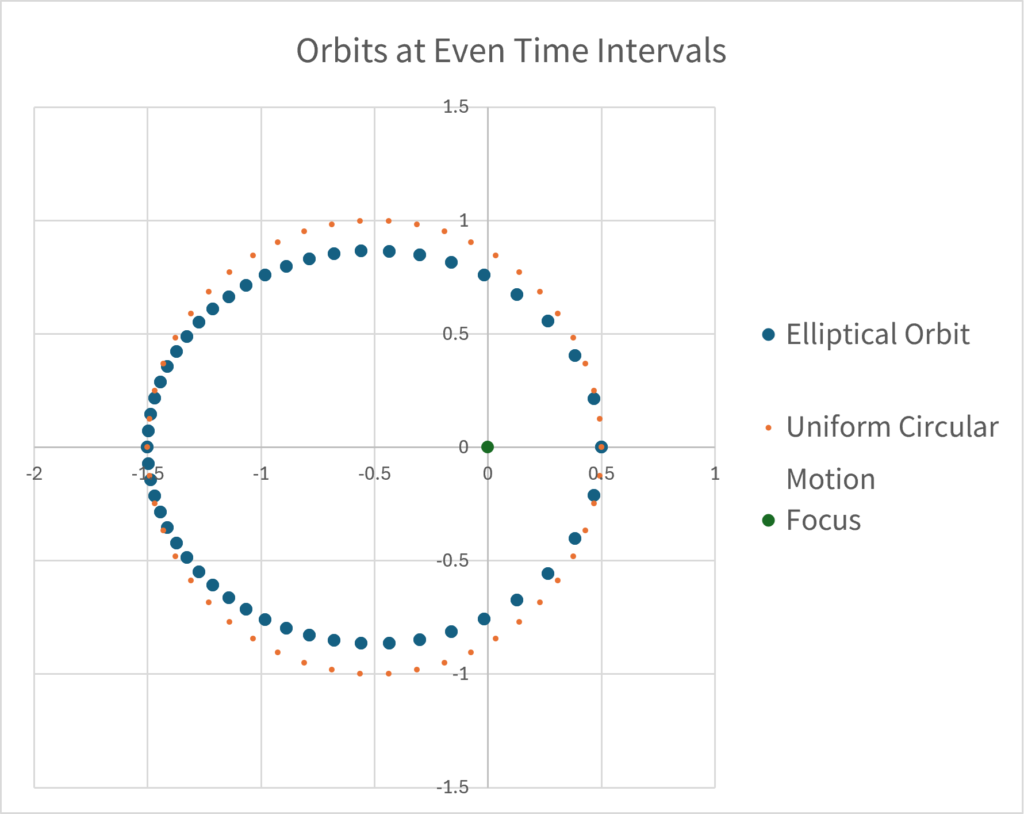
Finally, if we plot the coordinates for an equal time interval as a graph, we get the following. You can see that the speed tends to slow down as it move away from the focus.
Reference
[1] Bowman, Frank, Introduction to Bessel Functions, Dover Publication Inc., 1958.
[2] Watson, George N., A Treatise on the Theory of Bessel Functions Second Edition, Cambridge University Press, 1944.




Comments