*The painter ChatGPT “A dynamic and detailed illustration of a Texas Hold’em poker game in progress.”
Texas Hold’em and Kelly Criterion
In my last post, I believe I was able to develop the framework of the rules for Texas Hold’em. However, the opposing players simply place bets randomly, which is unlikely to be human and we can assume that they are fairly weak players. Therefore, let us consider a opposing player who, like a human, estimates his or her chances of winning from the cards in his or her hand and the community cards, and then makes optimal decisions based on that estimate.
First, there is a way to estimate the winning rate from the hand and community cards, which can be done using a Monte Carlo simulation. After doing this 10,000 times, it will converge to an almost correct answer, so an algorithm can be developed to determine the amount to bet based on this. As discussed in previous posts, this can be achieved by using the Kelly criterion or a CRRA-type utility function. For several reasons, artificial intelligence in Texas Hold’em appears to use a utility function that is close to risk-neutral, but natural human judgment can be predicted to be appropriately risk-averse. Therefore, in this article we consider decision-making with a risk-averse utility function.
The symbols used are defined as follows:
- \(\small p\): Estimated probability of winning
- \(\small \alpha\): The profit you will get if you win (odds)
- \(\small \beta\): The total chips put into the pot by players who have already folded
- \(\small n\): Number of players who are not currently folded
- \(\small W\): Your (the decision-maker’s) chips held before the start of play
- \(\small b\): Your chips already in the pot
- \(\small c\): Current rate (how many chips you need to put in to call)
- \(\small m\): Minimum raise (minimum bet) chips
First, consider how to determine the amount to bet according to the Kelly criterion (logarithmic utility function). In Texas Hold’em, the odds can be calculated as
\[ \small \alpha = n(fW)+\beta, \]
assuming that the number of players remaining in the chips put in by players who have already folded, \(\small \beta\), and that they will bet the same amount as you, \(\small n\). Let us find the optimal betting ratio \(\small f\) (amount of chips \(\small fW\)) in this case.
If you have already put \(\small b\) chips into the pot, the utility function when folding can be calculated as:
\[ \small E[U_{\text{Fold}}] = U_{\text{Fold}} = \ln\left(1-\frac{b}{W}\right). \]
If the current bet amount is \(\small c\leq W\), then if you call (check), you have to put in that amount of chips, so the expected utility can be calculated as:
\[ \small E[U_{\text{Call}}] = p\ln\left(1+\frac{\alpha-c}{W}\right)+(1-p)\ln\left(1-\frac{c}{W}\right). \]
Finally, when raising, the amount must be at least the current bet plus the minimum raise \(\small m\). However, you can choose the optimal raise amount from these, so the solution to optimization problem:
\[ \small \begin{align*} E[U_{\text{Raise}}(f)] &= \max_{fW \geq c+m} p\ln\left(1-f+\frac{\alpha}{W}\right)+(1-p)\ln(1-f) \\ &= \max_{fW \geq c+m} p\ln\left(1-f+nf+\frac{\beta}{W}\right)+(1-p)\ln(1-f) \end{align*} \]
will be the optimal raise amount. This can be solved analytically by calculating \(\small f\) that satisfies
\[ \small \frac{\partial }{\partial f}E[U_{\text{Raise}}(f)] = p\frac{n-1}{1-f+nf+\beta/W}-(1-p)\frac{1}{1-f}=0. \]
Rearranging the equation,
\[ \small f^{\ast} = \max\left\{\frac{np-1}{n-1}-\frac{1-p}{n-1}\frac{\beta}{W}, 0 \right\} \]
is the solution. The final decision is made by calculating the expected utility for each of Fold, Call, and Raise, and then deciding the option with the highest value as the NPC’s action. When raising, it is best to choose a cut number that is closer to the optimal \(\small f^\ast\). Note that in the case of \(\small f^\ast W<c+m\), we need to compare the utility function at the minimum raise amount.
One concern is that in Texas Hold’em, you have four decision-making opportunities, and once you raise your bet, it cannot be lowered. Therefore, strictly speaking, it must be solved as a dynamic optimization problem. Hence, maximizing the static utility function at each decision round may appear to be a more aggressive behavior than the original utility function. However, in the game, for the time being, we will simply make the optimal choice at each decision-making round. Also, the Kelly criterion does not allow all-ins, but it seems unnatural to always fold when going all-in after having put a lot of chips into the pot. Therefore, when calculating utility, it may be better to use \(\small W\) as the actual amount of chips held plus a certain value (adding a 1% to 5% margin).
In the Case of CRRA-type Utility Function
The Kelly criterion calculation can be easily extended to a CRRA-type utility function, so let us do some calculations. It is good for NPCs in a game to have a variety of players, such as risk-averse players and aggressive bettors, so it is a good idea to make them able to make decisions based on their level of risk aversion.
Since the CRRA utility function was:
\[ \small u(w) = \left\{ \begin{array}{ll}\frac{w^{1-\gamma}-1}{1-\gamma},& \quad \gamma \neq 1 \\ \log(w), & \quad \gamma=1 \end{array}\right., \]
the expected utility of folding and calling can be calculated as:
\[ \small \begin{align*} &E[U_{\text{Fold}}] = \frac{(1-b/W)^{1-\gamma}-1}{1-\gamma} \\ &E[U_{\text{Call}}] = p\frac{(1+(\alpha-c)/W)^{1-\gamma}-1}{1-\gamma}+(1-p) \frac{(1-c/W)^{1-\gamma}-1}{1-\gamma}, \end{align*} \]
respectively. The optimization problem for raising can be represented as:
\[ \small E[U_{\text{Raise}}(f)] = \max_{fW \geq c+m} p\frac{(1-f+nf+\beta/W)^{1-\gamma}-1}{1-\gamma}+(1-p)\frac{(1-f)^{1-\gamma}-1}{1-\gamma}. \]
When differentiated with respect to \(\small f\), we get
\[ \small \frac{\partial }{\partial f}E[U_{\text{Raise}}(f)] = p\frac{n-1}{(1-f+nf+\beta/W)^\gamma}-(1-p)\frac{1}{(1-f)^\gamma}=0, \]
so we just need to calculate \(\small f\) that satisfies this equation. Rearranging the equation,
\[ \small \begin{align*} &f^{\ast} = \max\left\{\frac{\psi}{\psi+n}-\frac{1}{\psi+n}\frac{\beta}{W}, 0\right\} \\ &\psi = \left(\frac{p(n-1)}{1-p}\right)^{\frac{1}{\gamma}}-1 \end{align*} \]
is the solution. The final decision is made by calculating the expected utility for each of Fold, Call, and Raise, and then deciding the option with the highest value as the NPC’s action. Using the above, we can determine players’ decisions based on their degree of risk aversion \(\small \gamma\).
Playstyle
There are other factors that determine a player’s behavior besides simply estimating the probability of winning and determining a betting strategy based on a certain degree of risk aversion. It is known that there are players who do not use the estimated probability of winning as is, but rather estimate the probability of winning to be more optimistic than the objective probability of winning, and conversely, there are players who estimate the probability of winning to be more pessimistic and only participate when they have a strong hand. There are generally four types of Texas Hold’em playing styles:
- Loose: Players who generally have a low probability of folding and a high participation rate
- Tight: Players who is more likely to fold if their hand is weak, and will only participate if their hand is strong.
- Aggressive: Players who raise aggressively and bet a high amount per play
- Passive: Players who have a low bet rate per play and fold when the bet rate becomes high
Using the concepts of this article, these can be defined as follows:
- Loose: Players who are upwardly biased in their estimates of their chances of winning
- Tight: Players who are downwardly biased in their estimates of their chances of winning
- Aggressive: Players with low risk aversion \(\small \gamma\)
- Passive: Players with high risk aversion \(\small \gamma\)
Loose/tight and aggressive/passive can be combined, making it possible to express playing styles that seem contradictory when viewed solely in terms of risk aversion, such as a tight and aggressive player or a loose and passive player.
If we estimate the subjective probability of winning with
\[ \small p^{\ast} = p^{(1-s)}, \]
\(\small s < 1\) is the style parameter, and \(\small s>0\) indicates a loose player, and \(\small s<0\) indicates a tight player.
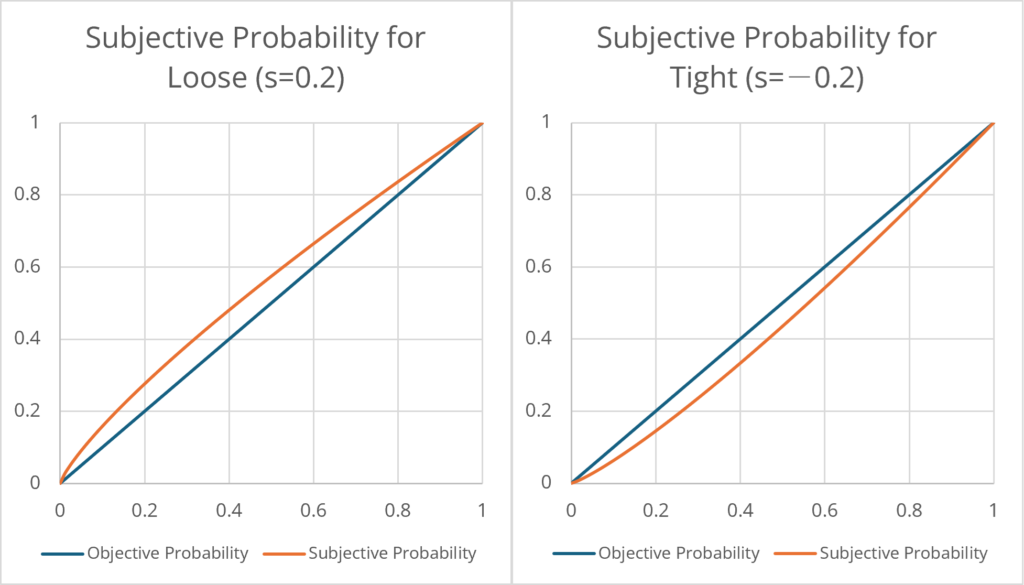
Also, being loose or tight may be different in the early stages (flop, pre-flop) and later stages (turn, river). It may be a good idea to set the preflop style parameter to \(\small s_p\) and the river style parameter to \(\small s_r\) and adjust it like:
- Pre-flop: \(\small s = s_p\)
- Flop: \(\small s = 2/3\times s_p+1/3\times s_r\)
- Turn: \(\small s = 1/3\times s_p+2/3\times s_r\)
- River: \(\small s = s_r\)
For example, if \(\small s_p>0\) but \(\small s_r=0\), the player will be a loose player in the early stages, but will be one who objectively evaluates probabilities in the later stages.
You might think that expressing the player’s personality by adjusting the calculated probability to apply a certain bias would weaken the NPC. This means basing your betting strategy on incorrect probabilities, which of course will be weakened by large parameters. However, to a certain extent, it reflects the player’s personality (play style), and it is assumed that it does not necessarily lead to the weakening of the player. The reason for this will become clear from the next section.
Designing NPC Strength (Failure Example)
To create a game, it is necessary to design it so that the user has the strength (weakness) to defeat it. You’ll lose motivation if you’re facing an NPC that is too strong for you to defeat. Therefore, the decision-making logic of the NPCs actually implemented must be somewhat weak or have flaws. Well, the main reason people play games is probably to complete them and gain a sense of self-affirmation. I implemented the NPC logic using the above specifications (Kelly criterion) and tried playing against it myself, but to be honest, it ended up being so strong that it was beyond the level that I (who only recently learned the rules) could not compete with. If I let my guard down, the bet would be raised immediately, and at that very moment, I felt that my opponent’s hand was strong. When I get a strong hand, I want to grab a lot of chips at once, but if their hand is weak, it will fold in an instant and I will not be able to get any chips. So, the purpose of this section is to weaken this program because it is so unpleasant.
Then, I thought to myself, “It must be strong because it can accurately predict the probability, and if I can interfere with this, I can weaken it.” To do this, we need to model the error in the probability estimate, which can be easily achieved by modeling the estimated true probability \(\small \bar{p}\) with normally distributed noise. In other words, we can simply assume that it is
\[ \small p = \bar{p}+\epsilon, \quad \epsilon\sim N(0,\sigma^2) \]
and round the value so that it satisfies \(\small 0 \leq p \leq 1\). By setting the estimation error \(\small \sigma\) to be larger for opponents with lower level, it will be possible to express the strength of each player.
After implementing it and trying it out, I feel like it has become even more brutal in the sense that it makes it harder to predict opponent’s hands and actions. In fact, when I pitted NPCs using the Kelly criterion, which has probability estimation error, against those using the Kelly criterion, which has no estimation error, the results were roughly equal; however, to the human eye, the former is more deadly in the sense that it makes it harder to understand the relationship between the hand and the bet, making the NPC’s actions more difficult to predict. Thinking about it this way, we might say that being able to accurately estimate the probability of winning contributes to strength up to a certain point, but beyond a certain point it contributes very little.
In the previous section, we stated that expressing a player’s playing style by applying a certain bias to the calculated probability does not necessarily lead to weakening. The reason for this is that if we can determine to a certain extent that strong hands are strong and weak hands are weak, as described above, then even if the probability deviates slightly from that, it will not have a significant impact on the player’s own strength. If you’re a Texas Hold’em player wanting to improve, the first thing you should do is learn the correct odds of winning in various situations, and at first it can make you feel like you’re improving. However, once you reach a certain point, isn’t it possible that pushing it to the limit doesn’t improve your player skill, and you hit a wall? If you have acquired the ability to correctly estimate your chances of winning, but you still feel like you are a weak player, you should consider the following possible issues.
Source of Weakness of Beginner Players
The most effective way to get to heaven is to know the way to hell.
Niccolò Machiavelli
The content of the previous section shows that the idea that the source of weakness lies in the inability to estimate the correct probability of winning is a correct hypothesis to a certain extent, but is actually incorrect. Despite this, there seems to be a clear difference between strong and weak players in this game, and this is probably why it is played competitively. So what is the difference between a player who feels strong and a player who feels weak? One hypothesis is that even if weak players correctly estimate their probability of winning, they do not take appropriate actions based on that probability.
For example, when playing Texas Hold’em with four players, you might bet 5% of your chips because you received a strong hand in preflop, but when the flop comes around your expectation turns out to be wrong, and because you still have a strong hand, you might assess your chances of winning as 20%. At this point, another player raises until 15% of your chips. How would you act in this situation? The options would be either
- Fold and cut loss for 5% of your chips.
- Call and bet chips of +10% (total 15%).
Perhaps most beginner players would choose option 2. Even though your plan didn’t work out, you may felt it was a waste to accept a 5% loss when you still had a 20% chance of winning. Even if you evaluate it based on expected value, it would be an
\[ \small \begin{align*} &E[W_1] = 0.95 \\ &E[W_2] = 0.2 \times 1.45 + 0.8 \times 0.85 = 0.97, \end{align*} \]
and you might think that this is reasonable. The reason why this behavior is inappropriate is that your level of risk aversion is unlikely to be risk-neutral (\(\small \gamma=0\)) in the first place. If we consider this problem using the Kelly criterion (which is still significantly lower than the risk aversion of the average person), the answer is:
\[ \small \begin{align*} &E[U(W_1)] = \ln(0.95) = -0.05129 \\ &E[U(W_2)] = 0.2 \times \ln(1.45) + 0.8 \times \ln(0.85) = -0.0557, \end{align*} \]
and folding would be the right choice.
On the other hand, let suppose that if the flop, turn, and river bring up the common cards you expect, you estimate that you have an 80% chance of winning. In this case, how much should you bet on the river? Most people would probably think of it as around 15% to 20% of the chips they have. This is the result for average risk aversion \(\small \gamma=5\). On the other hand, if you follow the Kelly criterion, your answer would be
\[ \small p = \frac{np-1}{n-1} =\frac{4 \times 0.8 -1}{4-1} = 0.7333 \]
and you should bet close to 70% of your chips. In short, a player who bets only 15% to 20% in this case and does not cut his losses in the previous example shows an inconsistent attitude towards risk.
In summary, what tends to happen to weak players is that they often have problem:
- Becoming less risk averse (or more risk seeking) when it comes to bets with low odds of winning or low expected returns.
- Becoming more risk averse when it comes to bets with higher odds of winning or higher expected returns.
If we consider why people buy lottery tickets, it is relatively easy to imagine that this tendency is more prevalent among people who like gambling. The author surmises that in Texas Hold’em, players who have a consistent attitude towards risk are more likely to be strong players, regardless of their level of risk aversion. Therefore, in order to weaken an NPC, it is sufficient to express the degree of risk aversion as a function of the probability of winning \(\small p\) (or the expected return \(\small p\alpha-c\)) in the form \(\small \gamma(p), \gamma'(p) > 0\). If we define the magnitude of the slope of risk aversion relative to the probability of winning as the player’s weakness, we can express the strength of the NPC.
As a specific functional form, the degree of risk aversion when the expected return is 0 (\(\small p=c/\alpha\)) is expressed as \(\small \bar{\gamma}\), and the inconsistency toward risk is represented by the parameter \(\small \lambda\). Then, if we define it as:
\[ \small \gamma(p, \alpha) = \max\left\{\bar{\gamma} + \lambda\left(p-\frac{c}{\alpha} \right), 0 \right\}, \]
we can express a player’s weakness as (\small \lambda) as discussed above.
Objective Probability and Subjective Probability
We have already explained that an inconsistent attitude toward risk is a sign of weakness as a player, but we can also assume that inexperienced players have a certain bias when it comes to estimating the probability of winning. This is the tendency to underestimate the probability of losing when the probability of losing is high, and to underestimate the probability of winning when the probability of winning is high. This property is known in behavioral economics as prospect theory.
As a concrete example, let us denote the probability of the expected return being zero as \(\small p_e\), and assume that a player estimates his probability of losing to be no lower than \(\small p_l=\delta p_e, 0\leq\delta\leq 1\). Conversely, suppose the player estimate that his probability of winning is also no greater than \(\small p_u=1-p_l\). In other words, for objective probability \(\small p \in [0, 1]\), subjective probability is considered to only take values in the range of \(\small \xi\in [p_l, p_u]\). Then, let assume
- \(\small p=0 \; \Rightarrow \; \xi=p_l\)
- \(\small p=p_e \; \Rightarrow \;\xi=p_e\)
- \(\small p=1 \; \Rightarrow \; \xi=p_u\)
hold true. When subjective probability is expressed as a quadratic function of objective probability \(\small \xi(p)=ap^2+bp+c\), the coefficient of the quadratic function can be calculated as:
\[ \small \begin{align*} &a = \frac{p_e(p_u-p_l-1)+p_l}{p_e(1-p_e)} = \frac{p_l(1-2p_e)}{p_e(1-p_e)} \\ &b = p_u-a-c \\ &c = p_l. \end{align*} \]
As an example, if \(\small \delta = 0.8, p_e = 0.25\), the subjective probability relative to the objective probability can be expressed as shown in the graph below.
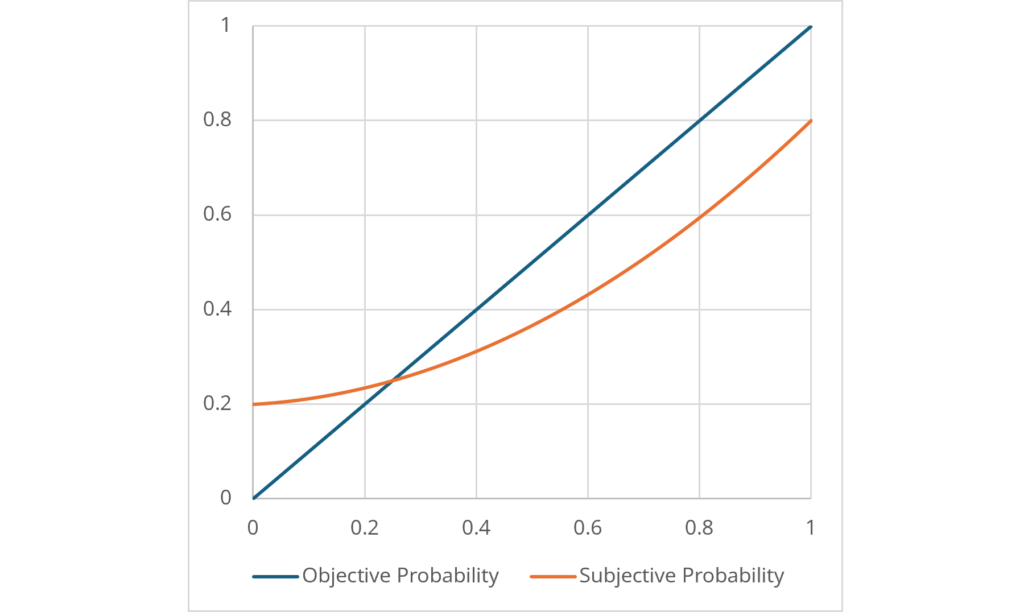
Unlike the players who are considered loose or tight as discussed in Section 3, the player’s weakness is likely due to the lack of consistency in his or her probability bias.
The weakness of players in Texas Hold’em is not due to their inability to correctly evaluate objective probability, but due to their making decisions based on subjective probability despite correctly evaluating the objective probability. If we bet based solely on our natural human emotions, we will likely exhibit trait:
- The probability of winning is evaluated based on subjective probability rather than objective probability.
- In games with negative expected returns, we become risk-loving, and in games with positive expected returns, we become risk-averse.
which will make us more likely to lose. The reason why computer-programmed NPCs feel so strongly about us is because they are free from these shortcomings. It may be difficult to correct this human tendency without conscious effort and considerable training.
Summary of NPC Parameters
From the above discussion, we can consider the parameters that determine the characteristics of a player to be as follows:
- Risk aversion \(\small \bar{\gamma}\)
- Style parameter(\(\small s_p\), \(\small s_r\))
- The slope of risk aversion with respect to the probability of winning \(\small \lambda\), and the deviation between objective probability and subjective probability \(\small \delta\)
We can add NPCs by specifying these parameters according to the chips the user owns (the user’s strength) or randomly. I have expanded the game again using the content up to this point.
Although some balancing will be necessary, it does seem like it is starting to have the appearance of a real game.
However, the truth is that there are still some things I am lacking as a Texas Hold’em player. For players at the intermediate level or above, it may not be that difficult to beat a player who is evaluated using the Kelly Criterion, which has no bias in estimating win probabilities (or is it just difficult, if not impossible?). I will explain this in my next post.




Comments