Antes and Preflop Strategy

*The painter ChatGPT “Artificial intelligence playing Texas Hold’em”

Preflop Strategy for Each Hand

Using the simulation created in the previous post:

we can find the strategy with the highest expected value when a specific hand is dealt. Let’s try that this time. The actual program I developed will be on the next page.

The calculations are too heavy for readers to try out themselves (parallel processing would be necessary if developing an actual solver), so I will show the results of my calculations, which took me several days to complete.

 As in the previous article, we will simplify the game and assume that all players check after the flop to determine the winner. The blinds are 10/20, each player’s stack is 180, and for raises, 2-bets are fixed at 60, and 3-bets are fixed at 180. If your opponent has a fixed strategy for a specific hand range, and you are dealt a specific hand, calculate the expected chip value for each of the following strategies.

1. 3bet/3bet…Raise to 3bet, passively call to 3bet.
2. 2bet/3bet…Raise to 2bet, passively call to 3bet.
3. 2bet/2bet…Raise to 2bet, passively call to 2bet.
4. 1bet/2bet…Limp in, passively call to 2bet.
5. 1bet/1bet…Limp in and fold if raised.
6. Fold

However, since I think there are many players who do not limp in, in this article I will ignore 4. and 5. and look for strategies. (When I calculated it, I found that there is a hand with the highest expected value for 1 bet/2 bet, but this may be due to the author’s simplification of the game. In reality, however, there may be many cases where it is better to limp in.) Each strategy is colored below for ease of understanding.

1. 3bet/3bet…Red
2. 2bet/3bet…Blue
3. 2bet/2bet…Green
4. Fold…Grey

In the Case of No Ante

First, let’s calculate the optimal strategy for the tight-aggressive player model. We assume that the tight-aggressive player adopts the following strategy (we simply set the hand ranges in descending order of win probability so that the VPIP is about 20% in order to ignore post-flop strategies).

	3bet/3bet	2bet/3bet	2bet/2bet	Fold
TAG	10%, 2players	20%, 2players	None	Otherwise

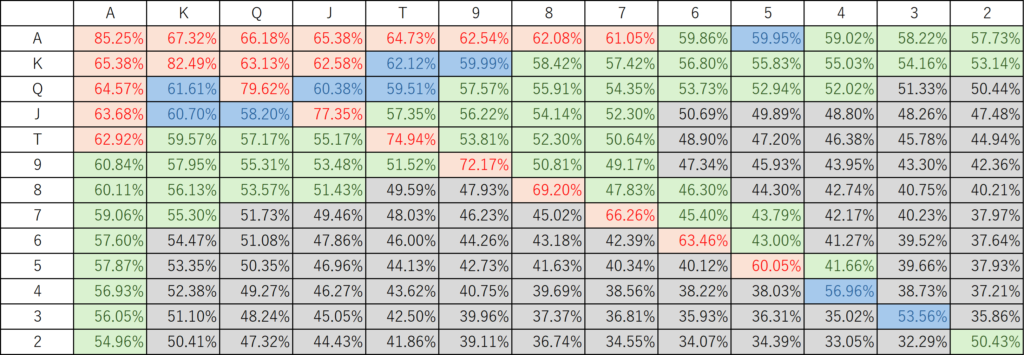
The actual strategies for each hand are as follows:

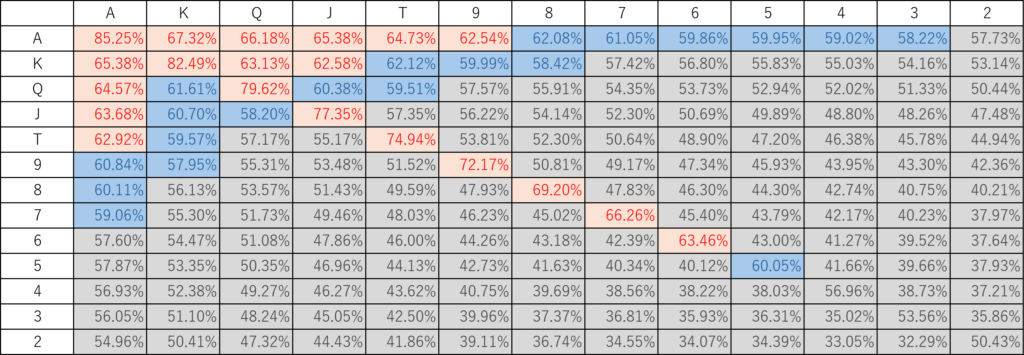
Assume there are six players and that all other players are using the betting strategies listed above. In this case, the optimal strategy for each hand is as follows:

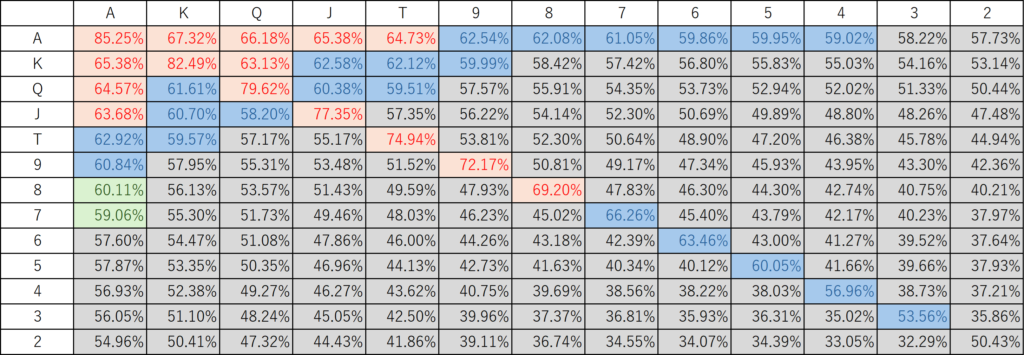
Although there are some differences, it generally seems best to adopt the same hand range and betting strategy as your opponent. In this sense, we can surmise that in games without antes, an equilibrium strategy would be to narrow your hand range so that your VPIP is around 20%. In games without antes, there is no penalty for folding other than SB and BB, so folding weak hands is the appropriate course of action.

 On the other hand, what would be the optimal strategy if there was an ante and your opponent narrowed their hand range to 20%? Let’s assume the ante is 0.25bb. If we calculate this, we get the following strategy.

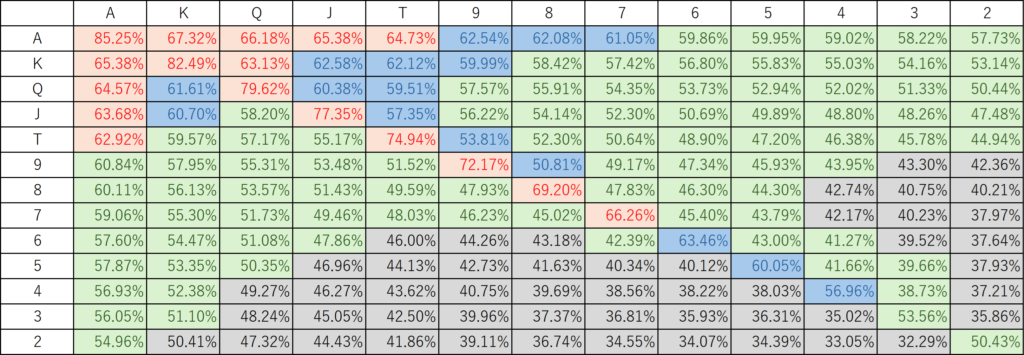
Entering with a wide range of hands seems like a strategy that maximizes expected value. In short, when the ante is as high as 0.25bb, a strategy of narrowing your hand range until you have a 20% VPIP is folding too much and can be exploited by playing looser. The above strategy is close to a VPIP 60% strategy using a 4-player table as the winning percentage table. If the ante is 0.25bb, a rare phenomenon may occur in which a player who has studied poker books and narrowed down his hand range to 20% is taken advantage of by a beginner-like player with a VPIP of around 60%. In fact, when I first started playing the game, I felt that I wasn’t very strong even when I limited my VPIP to 20%, but this may have been due to the ante.

Ante and VPIP

As mentioned in the previous section, when there is an ante, the optimal strategy does not seem to have a VPIP of 20%. In the game I play, there is an ante of 0.25bb, so the VPIP needs to be adjusted higher. Perhaps the game is designed to increase participation so players can enjoy the game in a short amount of time, and the higher the antes, the higher the participation rate, so the game tends to be more about luck than skill. If there is a big difference in the skill of the players, it may be inconvenient for attracting customers to the game. In the case of casinos that do not allow professional players, the ante may be set quite high.

 So how much VPIP should you adjust? According to ChatGPT, it is a good idea to enter so that your VPIP increases by about 4% for every 0.1bb increase in the ante. Copy and paste the table, it seems that

Ante	The Guideline of VPIP
No ante	18～22%
0.1bb	22～26%
0.2bb	25～30%
0.3bb	28～34%
0.5bb	32～40%

is the guideline. In the game I’m playing, a VPIP of about 30% seems to be the equilibrium strategy. However, when I calculate it using a calculator I made, it seems like the equilibrium strategy is about 40%. Finally, let’s check the results of these calculations.

In the Case of Ante Is 0.25bb

Let’s find the optimal preflop strategy for a 0.25bb ante against five players who have the following strategies:

	3bet/3bet	2bet/3bet	2bet/2bet	Fold
Aggresive	10%, 2players	20%, 2players	40%, 4players	Otherwise

The actual strategies for each hand are as follows:

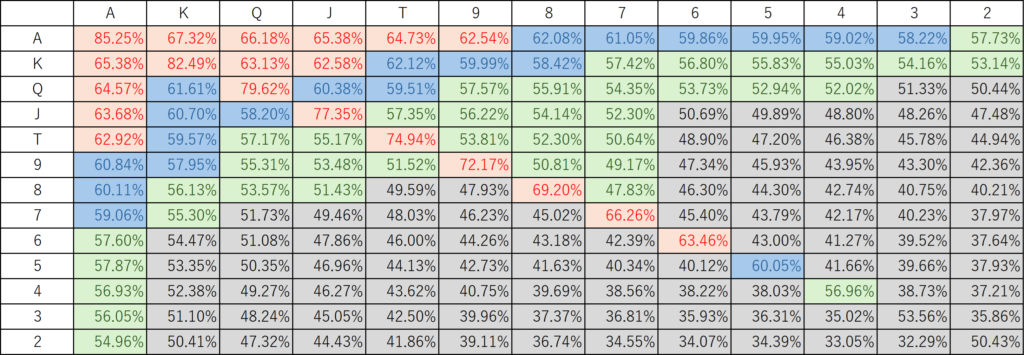
In this case, the optimal strategy for each hand is as follows:

It seems that the range of optimal strategies is slightly wider than that of the opposing player, but it looks like the equilibrium strategy would be around 40% VPIP. As this shows, the optimal preflop strategy seems to vary greatly depending on the ante level, so it is important to note that you will need to adjust your VPIP level depending on the rules of the game you are playing.

 Also, when the ante is 0.25bb, it appears that for low-ranked suited hands, there is generally not much difference in expected value between folding and entering with a 2bet/2bet, or entering with a 2bet/3bet. Perhaps these hands can be strong when you get two pair or better, but the probability of this happening doesn’t really correlate with the rank. The conclusion seems to be that you can generally fold low-ranked suited hands, and that entering 2bet/2bet doesn’t add much to your expected value. If you’re confident you can play well, you can call a 3bet. If there is an ante of 0.25bb, my beginner-like strategy of entering all suited bets may have some rationality. Well, I feel that entering all bets is a bit too much though…

Can the Equilibrium Strategy Be Calculated Systematically?

From the discussion so far, we have seen that the hand range to be adopted varies greatly depending on the game rules such as the ante. Therefore, we feel that we need a mechanism that can systematically derive the optimal strategy under given conditions. In this article, we fixed the opponent’s strategy and performed calculations, so we were able to determine the optimal betting strategy by simply running Monte Carlo simulations. Is it possible to find the optimal betting strategy under the assumption that your opponent will adopt the same optimal betting strategy as you, as in the Nash equilibrium strategy in game theory? In fact, this seems to be calculated using an algorithm called Counterfactual Regret (CFR) Minimization, which I will briefly introduce once I have a better understanding of it.

 In addition, counterfactual regret minimization estimates the betting strategy as a mixed strategy, but what if we want to find an equilibrium strategy as an optimal pure strategy, as in this article? In this case, where there are four possible strategies that can be adopted for each hand and it is necessary to determine them for 169 possible hands, we would be solving a combinatorial optimization problem to find the optimal strategy from among \(\small 4^{169}\) combinations. This is probably the same as the AI ​​for chess and shogi, and will use deep reinforcement learning (DQN) to search for a solution. It is difficult to find a solution with a simple homemade program like the author, so we have no choice but to give up. If you are confident that you are a master of machine learning, why not give it a try?